卷积神经网络（CNN）笔记

---

简单描述

Convolutional Neural Networks(CNN)，卷积神经网络主要是为了去解决计算机视觉上的问题，实际上，就是因为 CNN在计算机视觉上的成功应用，才让它变得这么火。

学习CNN，不光是为了在计算机视觉上的处理，更为重要的是去理解神经网络中蕴含的道理，事实上， 会觉得神经网络越来越像是一个搭积木的过程，有着各式各样的积木，你以随意的顺序或结构去搭建它们， 然后就得到了各式各样的神经网络类型。

CNN的结构

CNN其实与全连接神经网络并没有什么太大的区别，它只是在全连接的神经网络中加入了一种新的连接层，卷积层。

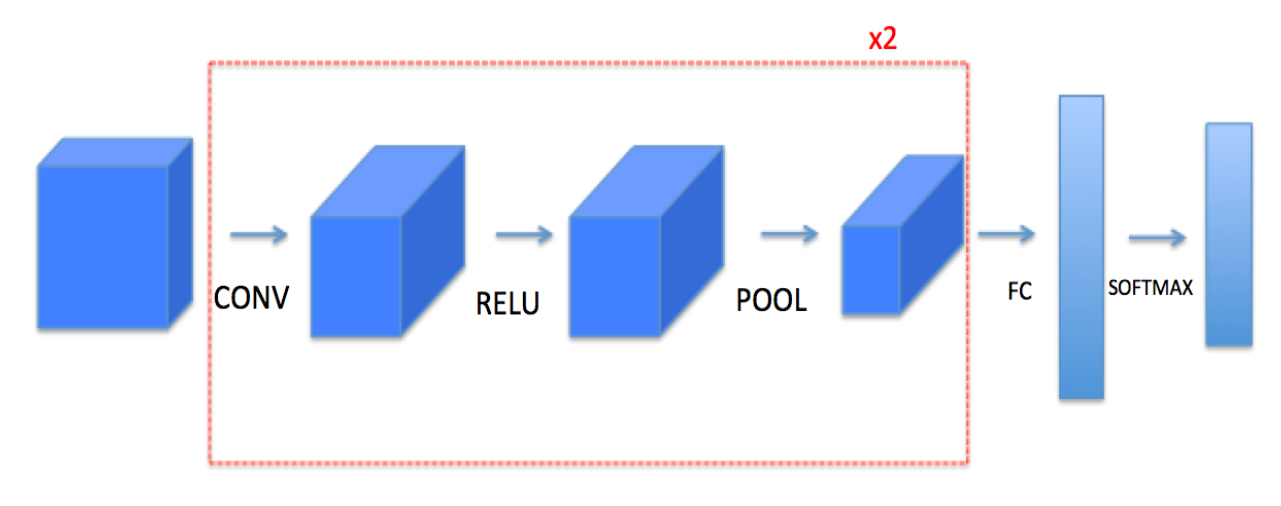
如上图，网络先进过一层卷积层（CONV），然后通过一个RELU激活函数，再通过一个POOL层，最后输入到后面的两层全连接层。

通常CNN的结构就与上图一样，网络首先是一系列的卷积层（包括激活函数与POOL），在网络的最后跟着连接几层的全连接层。

卷积层

这里引用到吴恩达课程作业中的一段演示视频，这一段视频十分的形象，这里引用到它：

如上面的视频所示，可以把输入层看作一个矩阵，它的维度为n_H_prev * n_W_prev * n_C_prev（这里先考虑单独一个样本的情况）， 如果这是从输入层开始的话，其中n_H_prev * n_W_prev就可以看成输入图片的长宽， 那么n_C_prev在图片是彩色的情况下就等于3，也就是RGB三个通道，如果是灰度图，那它就为1。 从英文上来说就是Height、Weight、Channel。

从视频中可以看到这个卷积层中有两个Filter，它们之间的运算完全没有关系，对于一个Filter来说，它在输入矩阵上从左上角开始， 左右滑动求取到值，每一次滑动就计算得到一个对应的值。在视频中它计算完毕后就得到一个3x3的输出。

通常情况下，所有Filter的维度都是一样的，视频中Filter的维度为f * f * n_C_prev，它的深度要与输入的Channel数一致 才能正常的进行计算，所有这里它的第三个维度为n_C_prev。设Filter对应的输入矩阵上的小格子为 $X$，Filter表示为$F$， 那么它们之间的计算公式为：

$$output = bias + \sum_i^f \sum_j^f \sum_k^{C} X_{(i,j,k)} * F_{(i,j,k)}$$

简单来说，就是两个矩阵做点积，然后求和，最后加上一个bias。那么对于一个Filter来说， 它就有 $f \times f \times C + 1$ 个参数。

最后将每一个Filter计算得到的结果作为一个Channel，叠在一起，就组成了最后的输出结果。

Padding

通过上面的计算步骤，只要Filter的长宽不是1，输出矩阵的长与宽就一定比输入矩阵的长与宽要小，并且对于矩阵角上的值来说， 它们参与运算的次数是没有矩阵内部的值参与的次数多的。

为了不让矩阵长与宽一直变小，让所有值相对公平的参与计算，就可以使用到Padding操作。

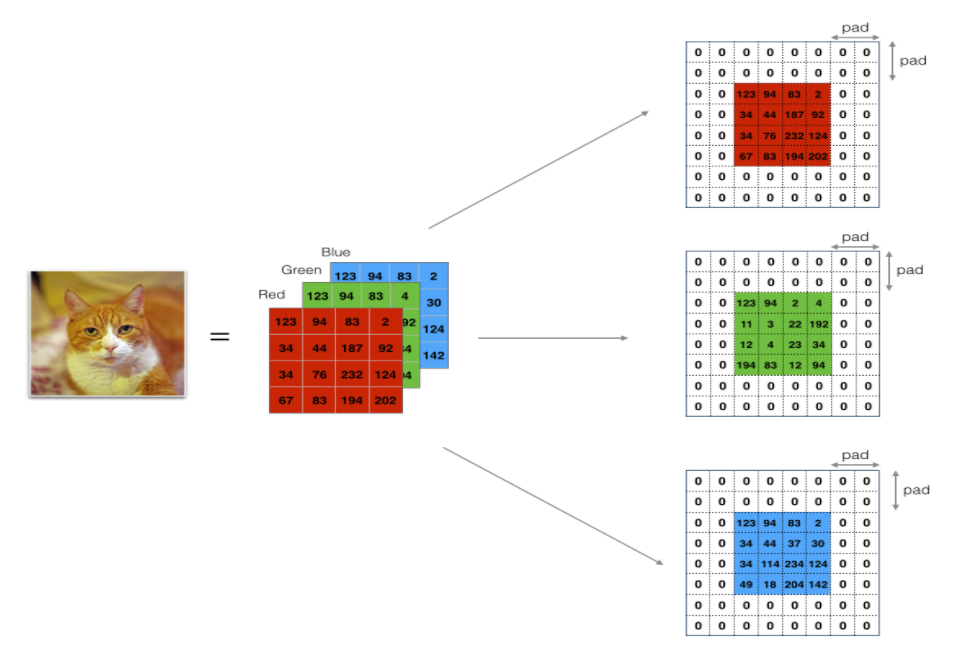
它的操作十分简单，就是在矩阵四周补零就可以了。

通常的深度学习框架中，例如TensorFlow，它在卷积层的参数中可以直接设置padding，它有两个取值valid和same， 其中valid就表示不进行padding，same则是表示进行padding，并且padding的大小刚好保证输入输出的维度大小相同。

stride

如上面所说，Filter在图片上进行滑动，那么滑动的距离就由stride来定义，通常它取值为1或2。

输出维度

进过上面的一顿操作，输出的维度为多少呢？随便就可以推出来，计算输出的维度公式如下：

$$n_H = \left \lfloor \frac{n_{H_{prev}} - f + 2 \times pad }{ stride } \right \rfloor + 1$$

POOL层

POOL层总是接在卷积层的后面，那么它到的是在干嘛的，它为什么要取名字叫做POOL？在学习卷积神经网络之前一直以为这一层很复杂， 但是实际上，这一层的操作十分简单。

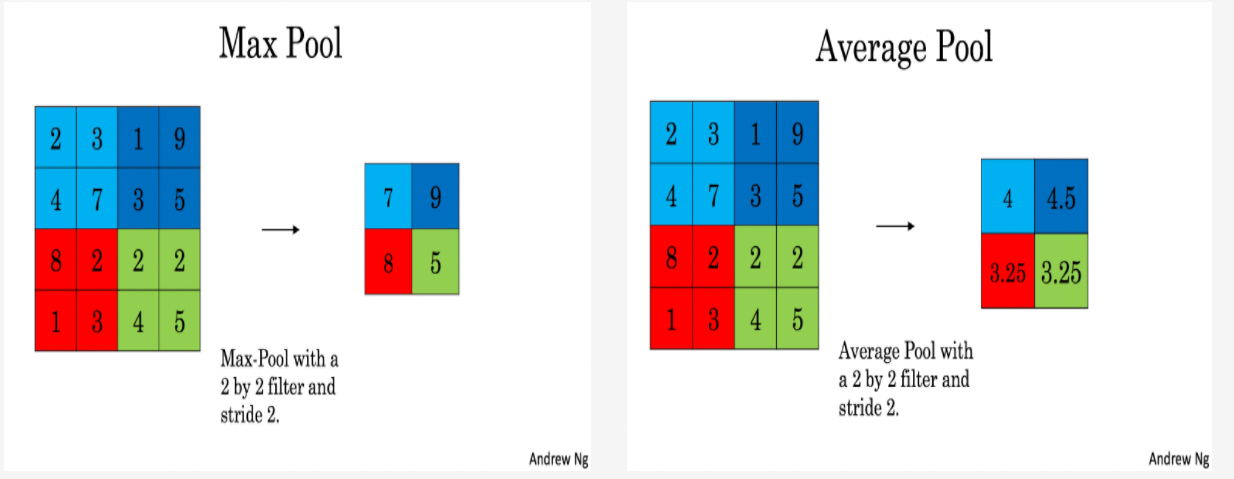
如上图所示，左边是Max Pool，右边是Average Pool，它和卷积层的操作几乎一样，也是滑动，每滑动一次计算出一个值。

它与卷积层操作的区别是它每次取得是区域内的最大值或者是平均值，也就是它计算出的结果只与输入矩阵有关系， 因为只有输入矩阵的值会参与运算。另外，它没有通道的概念，也就是它只有一个通道，所以它不是同时对输入矩阵的多个通道进行操作， 而是对输入的每个通道分别进行操作。

所以，输入与输出的维度进行比较的话，长宽通常会发生变化，而深度不会发生变化。

实际上，通常把POOL层理解为降低数据维度的方法。

卷积层在做神马？

在图像中，可以把每一个Filter看做一个特征的识别器（毕竟人家名字就叫做Filter），或许某个Filter的作用就是识别 一条直线，或者又是识别一个直角等。总之可以把一个Filter看成一个特征的识别。

事实上，全连接网络也能完成卷积层的作用，但是全连接层会带来太多的参数，另外，对于一个卷积层，不知要多少个全连接的网络层才能 完成与它相同的功能。所以卷积层的出现，带来了图像识别方面的巨大进步。

反向传播

其实卷积层与池化层的反向传播并不复杂。

首先注意到卷积层，对于它的一个输出值来说，它来源于输入的某一块与其中一个Filter运算后得到的结果，那么它对Filter 的求导，就能得到这个Filter的一个求导值。

这样一个一个求取，就能得到每个Filter的导数值，进而就能去更新Filter的权值。

对于POOL层，它的求导也十分简单，首先对于Max Pool，它的一个输出值来自与输入的一个值，那么直接把这个值传回就好。 对于Average Pool，它的一个输出值来源于很多个输入值，并且这些输入值对它的贡献是一样的，所以，将这个输出值平均传回就好。

未完待续？