前言
众所周知Java里面是没有指针的,但是有自动垃圾回收机制。C++是有指针的,但是没有自动垃圾回收。
Golang是一种新的语言,很多地方的设计借鉴了以前的语言,例如它是有指针的,并且有自动垃圾回收机制。
(主要代表着我需要进行指针的学习…)
Go语言基础学习
这方面去看一些教程就好:
首先菜鸟教程,内容不多,比较简单和基础:
然后可以看看知乎上是怎么推荐学习Go语言的:
然后还有官方的教程,有英文版的,也有中文版的,非常详细:
Documentation - The Go Programming Language
当然看上面的东西估计很快就烦了,那么不想看上面的就直接看官方提供的这个,真是个有意思的东西:
牛顿法(练习:循环与函数)
在教程练习:循环与函数中,要求我们实现一个求解平方根的函数, 方法就是使用牛顿法,代码如下:
1 | package main |
输出为:
1 | 561708 |
可以看到通过牛顿法,基本在10次迭代以内就可以计算出十分精确的平方根。
牛顿法原理:
牛顿法可以用于求解方程的根,当一个方程的根不好直接求解时,就可以使用牛顿法来进行迭代求解。
对于一个方程,需要求解 $x$ 的值:
那么首先利用泰勒展开来对 $f(x)$ 进行展开,这里从 $x_0$ 进行展开,并且只展开到一阶:
那么就可以使用这个近似式来求解原方程的近似解:
注意到 $f’(x_0)$ 就是原函数 $f(x)$ 在 $x_0$ 这点的斜率,那么其实在这一点上的切线方程就可以写为:
那么对于 $x = x_0 - \frac{f(x_0)}{f’(x_0)}$ 这一点,将它代入切线方程,求出它在切线上所对应的 $y$ :
也就是对应切线上的点 $(x_0 - \frac{f(x_0)}{f’(x_0)}, 0)$ ,画出图可以看出对应如下:
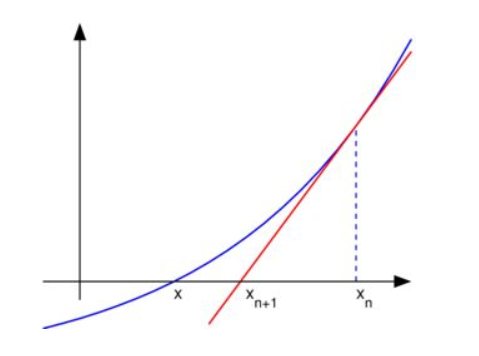
从图中可以看到观察到,这里所需要求解的点为曲线与x轴所相交的那个点 $x$ (y为0,也就是 $f(x)=0$ )。 虽然图中的 $x_{n+1}$ 并不是所需要求得点 $x$ ,但是它比 $x_n$ 更加接近 $x$ 。
所以这里就可以通过迭代来求解原方程的根,这一次从 $x_{n+1}$ 进行泰勒展开来求得下一个点。
回到练习题:
求解平方根,即方程 $x^2 = y$ 的解,即 $f(x) = x^2 - y$ ,代入上面的式子 $x = x_0 - \frac{f(x_0)}{f’(x_0)}$ , 可以推出:
题目中用的上面的形式,使用下面的形式其实也可以求解,但是两种方法的结果有细微的差别。 估计是考虑到溢出的问题吧,减法在这里可以保证更好的精度。
最大公约数与最小公倍数(练习题:最小众倍数)
最小众倍数:即是三个数的最小公倍数。
题目给了 a,b,c,d,e 一共5个数,求它们的最小众倍数中最小的那一个。
方法一:暴力搜索。复杂度等于搜索下限减去上限:
- 搜索下限:第3大的数。
- 搜索上限:前3小的数的乘积。
方法二:寻找所有三个数的组合的最小众倍数,取其中最小的那个。复杂度等于O(n^3),n为输入数的个数,本题 n = 5。
如何求3个数a,b,c的最小众倍数?
第一种求法:
- 求出
b*c,a*c的最大公约数A; - 求出
a*c,a*b的最大公约数B; - 求出A,B的最大公约数k;
- 使用
(a*b*c) / k即得到结果。
这个想法就是,对于 $C = abc$ :
假设最小众倍数为 $D$ ,那么 $C$ 一定是 $D$ 的整数倍 $k$,即 $C = kD$ :
也就是:
那么 $k$ 就是能同时整除 $bc,ac,ab$ 的最大的数,也就是它们的最大众约数, 也就可以通过 $bc,ac$ 的最大公约数 $A$ , $ac,ab$ 的最大公约数B,再求 $A,B$ 的最大公约数 $k$ 即可:
两个数的最大公约数求法在之前的博客中有写LeetCode 149 Max Points on a Line
第二种求法:
- 求出a,b的最小公倍数A;
- 求出A,c的最小公倍数D;
- D就是a,b,c的最小众倍数。
首先,对于a,b的最小公倍数A:
然后对于A,c的最小公倍数D:
上面合在一起,即:
注意到由于最小公倍数的性质,$x_1$ 与 $x_2$ 互质,$x_3$ 与 $x_4$ 互质。
如果 $D$ 是a,b,c的最小众倍数,则 $x_1 x_3$ ,$x_2 x_3$,$x_4$ 的最大众约数为 1 。
这里使用反证,假设 $x_1 x_3$ ,$x_2 x_3$,$x_4$ 的最大众约数不为 1 。
由于$x_3$ 与 $x_4$ 互质,那么只能 $x_1$ 、 $x_2$ 与 $x_4$ 存在不为 1 的最大公约数 $S$ :
也就是 $x_1$ 与 $x_2$ 存在最大公约数 $S$ ,与原条件 $x_1$ 与 $x_2$ 互质相矛盾。
所以 $x_1 x_3$ ,$x_2 x_3$,$x_4$ 的最大众约数为 1 ,即 $D$ 是a,b,c的最小众倍数。
同理,使用公约数的解法可以改写为:
对于两个数的最小公倍数:
对于a,b的最小公倍数A :
注意 $k_1$ 与 $k_2$ 互质,假如a,b的最大公约数为 $S$ :
注意到 $h_1$ 与 $h_2$ 互质,那么这里就可以推出:
注意 $k_1$ 与 $k_2$ 互质,$h_1$ 与 $h_2$ 互质,所以 $\frac{h_2}{h_1}$ 必然等于 $\frac{k_1}{k_2}$ ,所以:
所以:
即a,b的最小公倍数等于它们的乘积除以它们的最大公约数。
1 | func LCM(a, b int) int { |
代码,求一个数组的最小众倍数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
package main
const MinInt = int(^uint(0) >> 1)
func zbsUseGCD(seq *[]int) int {
min := MinInt
n := len(*seq)
for i := 0; i < n; i++ {
for j := i+1; j < n; j++ {
for k := j+1; k < n; k++ {
zbsTmp := findZBSUseGCD((*seq)[i], (*seq)[j], (*seq)[k])
if zbsTmp < min {
min = zbsTmp
}
}
}
}
return min
}
func zbsUseLCM(seq *[]int) int {
min := MinInt
n := len(*seq)
for i := 0; i < n; i++ {
for j := i+1; j < n; j++ {
for k := j+1; k < n; k++ {
zbsTmp := findZBSUseLCM((*seq)[i], (*seq)[j], (*seq)[k])
if zbsTmp < min {
min = zbsTmp
}
}
}
}
return min
}
func findZBSUseGCD(a, b, c int) int {
return (a*b*c) / GCD(GCD(a*b, b*c), a*c)
}
func findZBSUseLCM(a, b, c int) int {
return LCM(a, LCM(b, c))
}
func LCM(a, b int) int {
return (a*b) / GCD(a, b)
}
func GCD(a, b int) int {
var c int
for b != 0 {
c = a % b
a = b
b = c
}
return a
}
1 | package main |
练习:Web 爬虫
修改 Crawl 函数来并行地抓取 URL,并且保证不重复。
- 使用map和互斥锁来保证URL的唯一抓取。
- 使用管道或者
sync.WaitGroup来实现主线程等待子线程结束。
代码一:
1 | package main |
这里实现了SafeCounter结构体来实现线程安全的map,并在set函数中使用了defer来将解锁放到return之后。
Crawl函数使用了管道来让主线程等待子线程结束,但是可以看到这样写十分复杂,每个return之前都需要记得向管道写入。
可以使用下面方法简化:
1 | func WriteToChan(ch chan int) { |
这里编写函数WriteToChan,然后使用defer来实现函数结束时往管道写入。
当然也可以使用sync.WaitGroup:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
func Crawl(url string, sc *SafeCounter, fetcher Fetcher, ch chan int, wg *sync.WaitGroup) {
defer wg.Done()
if !sc.set(url) {
return
}
body, urls, err := fetcher.Fetch(url)
if err != nil {
fmt.Println(err)
return
}
fmt.Printf("found: %s %q\n", url, body)
var wgNext sync.WaitGroup
wgNext.Add(len(urls))
for _, u := range urls {
go Crawl(u, sc, fetcher, ch, &wgNext)
}
wgNext.Wait()
}
1 | func Crawl(url string, sc *SafeCounter, fetcher Fetcher, ch chan int, wg *sync.WaitGroup) { |
素数求解
素数或者质数:大于1,并且只能被1和自身整除的数,例如:2,3,5,7…
判断一个数 $n$ 是不是素数,可以按照定义:
- 方法一:从2开始判断是否能够整除,直到 $\sqrt{n}$ 。
- 方法二:如果比 $n$ 小的数所构成的合数中没有 $n$,那么 $n$ 是素数。
问题一:如何快速求解[0,n]范围内的素数。
如果n较大的时候,使用方法一复杂度也较大,这时使用方法二会更快:
1 | package main |
当然,这样的写法会有很多重复筛选,例如2*3,3*2都会被统计,但是其实没有必要。
另外,还有重复类似 4*2, 4*3, 4*4 ... 其实就是 2*4, 2*6, 2*8 ...,也就是说对于不是素数的数,
筛选它们的倍数是重复的。更进一步,这里只需要筛选素数的倍数就可以了。
按照上面所述,可以改写如下:
1 | func findPrime(n int) { |
相当于这里只统计:
2*2,2*3,2*4…3*3,3*4,3*5…5*5,5*6,5*7…
当然这里还是会出现重复,例如2*9和3*6,但是已经少了很多重复的筛选了。
更进一步,快速筛选法:
1 | func findPrime(n int) { |
这样在筛选过程中,可以不出现任何一个重复。
那么为什么这样可以不出现任何一个重复,且筛选出所有合数呢?
首先每一个合数都可以以唯一形式被写成质数的乘积,即分解质因数,那么只要是不同的质数组合,得到的肯定是不同的合数,
例如合数 $A_1 = a \times b \times c$ ,$A_2 = d \times e \times f$,假设 $a \leq b \leq c ; d \leq e \leq f$,
那么只有在 a == d && b == e && c == f 时, $A_1$ 等于 $A_2$。
那么在给定一个素数集合 {a, b, ..., n} ,就可以使用下面的方法来组合出所有这个集合所能表示的合数,且不发生重复:
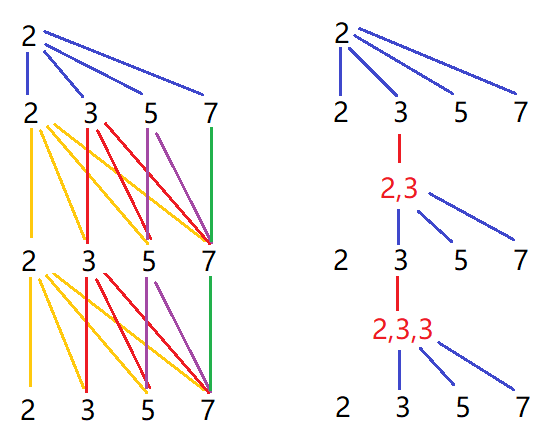
图中的集合为{2, 3, 5, 7},左边是包含2的所有合数的组合方法,右边是其中 2,3,3 这条路线的样子。
可以看到,第一层生成 {2,2},{2,3},{2,5},{2,7},对于后面的三个集合 {2,3},{2,5},{2,7} 来说,它们向下的路线无法再经过 2 ,
所有它们所生成的集合中,永远不可能包含子集 {2,2},所以 {2,2} 与 {2,3},{2,5},{2,7} 向下所得到的集合永远不会相同,
同理可以知道 {2,2},{2,3},{2,5},{2,7} 互相之间向下不可能生成相同集合,也就保证了不会重复。
至于覆盖所有合数,则是显然的,因为任何合数都可以表示为图中一条路线。
当然,另一种组合顺序也是一样的,也是快速筛选法中所用的:
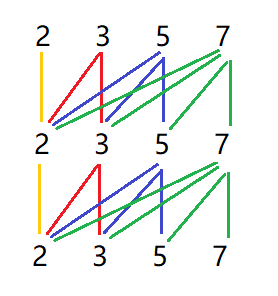
也就是刚才是限制向左,这里是限制向右,不过效果都是一样的。
为什么说算法中使用的就是这种组合方式呢?我们来跑100以内素数,打印一下输出就知道了:
1 | i = 2 |
可以看到,输出完全符合预期(因为本来就是按这个组合方法写的…):
- 当
i = 2,那么由于限制往右,那么向下只能再组合出{2,2}; - 当
i = 3,那么向下只能再组合出{2,2},{3,2}; - 当
i = 6,其实就是组合{3,2},相当于图中的 3 走到 2,那么再向下也只有 2 能选择了,所以只能组合出{3,2,2}; - …
所以这里的 i%primes[j] == 0 其实就是在判断 primes[j] 是不是 i 的最小因数,一旦判断为 true,就相当于到达了右边界,
所以进行 break。
所以这样的方法一定不会出现任何重复的筛选。
至于包含所有合数,那也是明显的,对于合数 $A = a \times b \times … \times m \times n$ ,假设 $ a \geq b \geq … \geq m \geq n$, 那么一定会先遍历到 $i = a \times b \times … \times m$ ,又因为 $i$ 向下组合的右边界为 $m$ ,且 $m \geq n$ ,所以,一定会由 $i$ 筛选出 $A$, 所以这里一定不会漏掉任何一个合数。
证明完毕。