龙

哇咔咔

0%

线段树(Segment Tree)进阶使用记录(HDU3397)

发表于 更新于 分类于 Disqus：
线段树的lazy标志的使用，实践题目HDU3397

线段树的进阶

在前一篇博客中线段树(Segment Tree)使用记录，介绍了基础的线段树形式。

这一篇讨论以下进阶的使用，主要针对lazy标志。

上一篇博客中对于一个区间的修改只是单点修改，但是有时候会碰到区间修改的情况，这时基本的线段树可能就不适用了。

这时就需要针对区间修改来对区间树的更新方式进行变化。

下面先假设问题为，初始给定一个数组：

  • 修改操作包括：区间加上一个数，或者区间减去一个数。
  • 查询操作包括：区间的求和。

建树

上一篇博客中使用的是至底向上的建树方式，这样的建树方法可以最大化空间利用率（2n空间即可），但是这样会造成一些处理上的困难，如图：

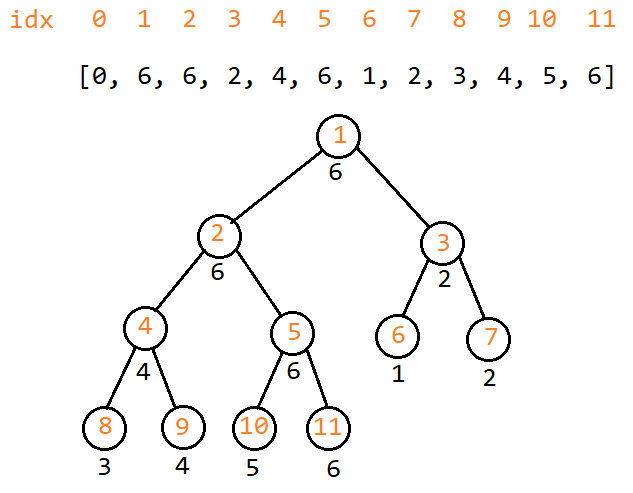
图中点1、2其实在整颗树的最右边，而3、4、5、6却在左边，这样的节点排列方式对于区间修改是不利的（会造成逻辑上的混乱）。

所以可以使用至顶向下的建树方式，也就是递归建树：

1
2
3
4
5
6
7
8
9
10
private void buildTree(int l, int r, int node, int[] arr) {
    if(l == r) {
        table[node] = arr[l];
        return;
    }
    int mid = (l + r) >> 1;
    buildTree(l, mid, left(node), arr);
    buildTree(mid+1, r, right(node), arr);
    pushUp(node);
}

将区间的左边放到左子树，右边放到右子树来进行递归建树，注意在建立完毕左右子树之后更新本节点信息（pushUp(node)）。

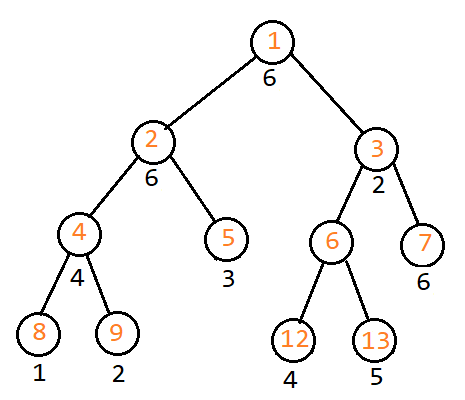
可以看到上面就是至顶向下所建立的树的结构，节点序号从左向右排列，但是这样带来的问题就是增加了空间占用（上图中数组大小14）。

1
2
3
4
5
6
7
8
9
10
public SegmentTreeLazySum(int n, int[] arr) {
    this.n = n;
    int i = 1;
    while (i < n) {
        i = i << 1;
    }
    table = new int[2*i];
    lazy = new int[2*i];
    buildTree(0, n-1, 1, arr);
}

可以使用上面的方式来确定所需数组大小，也就是假如最后一层需要能放下n个元素，最小的i使得$2^i > n$。

lazy标记

在进行区间修改时，我们不可能像单点修改一样，将所有节点的值都修改，因为在查询时，可能只需要上层节点的信息就可以完成查询。

例如将整个数组所有点都增加1，然后询问整个数组的求和，这时我们只需要在根节点上之前所记录的求和加上整个数组的长度即可。

这样的思想就是为了降低算法复杂度，对于一个区间的修改，我们先欠着，当必要的时候才进行修改。

update方法的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// [L, R]为原始更新区间，[x, y]为当前节点node所包含的区间
// t为操作类型，c为操作数
public void update(int t, int L, int R, int c, int x, int y, int node) {
    if ( y < L || x > R ) {
        return;
    }
    if (L <= x && y <= R) {
        c = t == 0 ? c : -c;
        table[node] += (y - x + 1) * c;
        lazy[node] += c;
        return;
    }
    lazyDown(node, y - x + 1);
    int mid = (x + y) >> 1;
    update(t, L, R, c,  x, mid, left(node));
    update(t, L, R, c, mid+1, y, right(node));
    pushUp(node);
}

这里lazy标记就代表需要加上的数（使用正负来代表原始的加减）。

可以看到：

  1. 当发现整个子区间都包含在更新区间中时，就可以停止更新下传，更新节点值与lazy标记即可。
  2. 当子区间部分包含在更新区间中时，就需要下传更新，那么此时就需要先将之前的lazy标记给下传了。
  3. 完成左右儿子的更新后，记得更新本节点（pushUp(node)）。

那么这里就涉及到了lazyDown函数，这个函数根据不同的情况会有很大的变化，这里因为只涉及加减法，所以比较简单：

1
2
3
4
5
6
7
8
9
10
11
private void lazyDown(int node, int len) {
    if (lazy[node] == 0) {
        return;
    }
    int l = left(node), r = right(node);
    lazy[l] += lazy[node];
    table[l] += lazy[node] * (len - (len >> 1));
    lazy[r] += lazy[node];
    table[r] += lazy[node] * (len >> 1);
    lazy[node] = 0;
}

因为只是加减法，所以子节点的lazy标记单纯加上父节点的lazy标记即可，当然同时也要记得更新子节点的值。

　查询操作

查询操作就递归向下即可，当然记得需要下传lazy标记：

1
2
3
4
5
6
7
8
9
10
11
12
13
public int query(int L, int R, int x, int y, int node) {
    if ( y < L || x > R ) {
        return 0;
    }
    if (L <= x && y <= R) {
        return table[node];
    }
    lazyDown(node, y - x + 1);
    int res = 0, mid = (x + y) >> 1;
    res += query(L, R, x, mid, left(node));
    res += query(L, R,mid+1, y, right(node));
    return res;
}

完整代码

注意这里所针对的问题，初始给定一个数组：

  • 修改操作包括：区间加上一个数，或者区间减去一个数。
  • 查询操作包括：区间的求和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
public class SegmentTreeLazySum {

    private int[] table;
    private int[] lazy;
    private int n;

    public SegmentTreeLazySum(int n, int[] arr) {
        this.n = n;
        int i = 1;
        while (i < n) {
            i = i << 1;
        }
        table = new int[2*i];
        lazy = new int[2*i];
        buildTree(0, n-1, 1, arr);
    }

    private void buildTree(int l, int r, int node, int[] arr) {
        if(l == r) {
            table[node] = arr[l];
            return;
        }
        int mid = (l + r) >> 1;
        buildTree(l, mid, left(node), arr);
        buildTree(mid+1, r, right(node), arr);
        pushUp(node);
    }

    private void pushUp(int node) {
        int l = left(node), r = right(node);
        table[node] = table[l] + table[r];
    }

    private void lazyDown(int node, int len) {
        if (lazy[node] == 0) {
            return;
        }
        int l = left(node), r = right(node);
        lazy[l] += lazy[node];
        table[l] += lazy[node] * (len - (len >> 1));
        lazy[r] += lazy[node];
        table[r] += lazy[node] * (len >> 1);
        lazy[node] = 0;
    }

    public void update(int t, int L, int R, int c, int x, int y, int node) {
        if ( y < L || x > R ) {
            return;
        }
        if (L <= x && y <= R) {
            c = t == 0 ? c : -c;
            table[node] += (y - x + 1) * c;
            lazy[node] += c;
            return;
        }
        lazyDown(node, y - x + 1);
        int mid = (x + y) >> 1;
        update(t, L, R, c,  x, mid, left(node));
        update(t, L, R, c, mid+1, y, right(node));
        pushUp(node);
    }

    public int query(int L, int R, int x, int y, int node) {
        if ( y < L || x > R ) {
            return 0;
        }
        if (L <= x && y <= R) {
            return table[node];
        }
        lazyDown(node, y - x + 1);
        int res = 0, mid = (x + y) >> 1;
        res += query(L, R, x, mid, left(node));
        res += query(L, R,mid+1, y, right(node));
        return res;
    }

    private int left(int idx) {
        return idx << 1;
    }

    private int right(int idx) {
        return (idx << 1) + 1;
    }
    
    // 测试用例：
    // 输入：
    // 1
    // 5 5
    // 1 1 1 1 1
    // 2 2 4 7
    // 1 1 3 4
    // 0 0 4 2
    // 1 1 4 8
    // 2 2 4 3
    //
    // 输出：
    // 3
    // -23
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int T = sc.nextInt();
        for (int k = 0; k < T; k++) {
            int n, m, t, x, y, c;
            n = sc.nextInt();
            m = sc.nextInt();
            int[] arr = new int[n];
            for (int i = 0; i < n; i++) {
                arr[i] = sc.nextInt();
            }
            SegmentTreeLazySum hdu = new SegmentTreeLazySum(n, arr);
            for (int i = 0; i < m; i++) {
                t = sc.nextInt();
                x = sc.nextInt();
                y = sc.nextInt();
                c = sc.nextInt();
                if (t == 2) {
                    System.out.println(hdu.query(x, y, 0, n - 1, 1));
                } else {
                    hdu.update(t, x, y, c,0, n - 1, 1);
                }
            }
        }
    }

}

HDU3397

这个题目是一个比较典型的线段树题，初始给定一个数组，操作包括：

  • 0：将区间[x, y]全部置为0；
  • 1：将区间[x, y]全部置为1；

  • 2：将区间[x, y]中的1变为0，0变为1；

  • 3：查询区间[x, y]中1的数量；

  • 4：查询区间[x, y]中连续出现1的最多的次数。

这道题的难点一在于查询4，因为在一个节点上，我们需要通过它的两个子节点的信息来得到连续1的数量。

对于这个问题，可以考虑这样来解决，在一个节点上，我们保存如下信息：

  1. 贴着区间左边的连续1的数量LLen。
  2. 贴着区间右边的连续1的数量RLen。
  3. 区间中的最大连续1的数量MLen。

那么对于一个节点，它的相关信息可以这样计算得到：

  1. LLen：等于左儿子的LLen。但是需要注意，如果左儿子的LLen等于整个区间的长度，那么就为左儿子的LLen加上右儿子的LLen。
  2. RLen：同上。
  3. MLen：等于 左儿子的MLen，右儿子的MLen，左儿子的RLen加上右儿子的LLen 的最大值。

这道题的难点二在于操作2，如何在一个节点上完成信息的更新，主要是LLen、RLen、MLen信息的变化？

为了完成这个件事，这里对称的将连续0的数量保存下来ZLLen、ZRLen、ZMLen，这样在进行操作2时， 就可以将LLen、RLen、MLen和ZLLen、ZRLen、ZMLen的信息交换即可。

整个代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
import java.util.Arrays;
import java.util.Scanner;

public class HDU3397 {

    private int[] table;
    private int[] Ztable;
    private int[] MLen;
    private int[] LLen;
    private int[] RLen;
    private int[] ZLLen;
    private int[] ZRLen;
    private int[] ZMLen;
    private int[] lazy;
    private int n;

    public HDU3397(int n, int[] arr) {
        this.n = n;
        int i = 1;
        while (i < n) {
            i = i << 1;
        }
        table = new int[2*i];
        Ztable = new int[2*i];
        lazy = new int[2*i];
        MLen = new int[2*i];
        LLen = new int[2*i];
        RLen = new int[2*i];
        ZLLen = new int[2*i];
        ZRLen = new int[2*i];
        ZMLen = new int[2*i];
        Arrays.fill(lazy, -1);
        buildTree(0, n-1, 1, arr);
    }

    private void buildTree(int l, int r, int node, int[] arr) {
        if(l == r) {
            table[node] = MLen[node] = LLen[node] = RLen[node] = arr[l];
            Ztable[node] = ZLLen[node] = ZRLen[node] = ZMLen[node] = 1 - arr[l];
            return;
        }
        int mid = (l + r) >> 1;
        buildTree(l, mid, left(node), arr);
        buildTree(mid+1, r, right(node), arr);
        pushUp(node, mid - l + 1, r - mid);
    }

    private void pushUp(int node, int lenL, int lenR) {
        int l = left(node), r = right(node);
        table[node] = table[l] + table[r];
        Ztable[node] = Ztable[l] + Ztable[r];

        LLen[node] = LLen[l] == lenL ? LLen[l] + LLen[r] : LLen[l];
        RLen[node] = RLen[r] == lenR ? RLen[r] + RLen[l] : RLen[r];

        ZLLen[node] = ZLLen[l] == lenL ? ZLLen[l] + ZLLen[r] : ZLLen[l];
        ZRLen[node] = ZRLen[r] == lenR ? ZRLen[r] + ZRLen[l] : ZRLen[r];

        MLen[node] = Math.max(MLen[l], MLen[r]);
        MLen[node] = Math.max(MLen[node], RLen[l] + LLen[r]);

        ZMLen[node] = Math.max(ZMLen[l], ZMLen[r]);
        ZMLen[node] = Math.max(ZMLen[node], ZRLen[l] + ZLLen[r]);
    }

    private void lazyDown(int node, int len) {
        if (len <= 1 || lazy[node] == -1) {
            return;
        }
        int l = left(node), r = right(node);
        lazyHelper2(lazy[node], l, len - (len >> 1));
        lazyHelper2(lazy[node], r, len >> 1);
        lazy[node] = -1;
    }

    private void lazyHelper(int node, int len) {
        if (lazy[node] == 0) {
            table[node] = LLen[node] = RLen[node] = MLen[node] = 0;
            Ztable[node] = ZLLen[node] = ZRLen[node] = ZMLen[node] = len;
        } else if (lazy[node] == 1) {
            table[node] = LLen[node] = RLen[node] = MLen[node] = len;
            Ztable[node] = ZLLen[node] = ZRLen[node] = ZMLen[node] = 0;
        } else if (lazy[node] == 2) {
            int tmp0 = table[node], tmp1 = LLen[node], tmp2 = RLen[node], tmp3 = MLen[node];
            table[node] = Ztable[node];
            LLen[node] = ZLLen[node];
            RLen[node] = ZRLen[node];
            MLen[node] = ZMLen[node];
            Ztable[node] = tmp0;
            ZLLen[node] = tmp1;
            ZRLen[node] = tmp2;
            ZMLen[node] = tmp3;
        }
    }

    private void lazyHelper2(int t, int node, int len) {
        if (t == 2) {
            if (lazy[node] == -1) {
                lazy[node] = t;
                lazyHelper(node, len);
            } else if (lazy[node] == 2) {
                lazyHelper(node, len);
                lazy[node] = -1;
            } else {
                lazy[node] = 1 - lazy[node];
                lazyHelper(node, len);
            }
        } else {
            lazy[node] = t;
            lazyHelper(node, len);
        }
    }

    public void update(int t, int L, int R, int x, int y, int node) {
        if ( y < L || x > R ) {
            return;
        }
        if (L <= x && y <= R) {
            lazyHelper2(t, node, y - x + 1);
            return;
        }
        lazyDown(node, y - x + 1);
        int mid = (x + y) >> 1;
        update(t, L, R, x, mid, left(node));
        update(t, L, R, mid+1, y, right(node));
        pushUp(node, mid - x + 1, y - mid);
    }

    public int query3(int L, int R, int x, int y, int node) {
        if ( y < L || x > R ) {
            return 0;
        }
        if (L <= x && y <= R) {
            return table[node];
        }
        lazyDown(node, y - x + 1);
        int res = 0, mid = (x + y) >> 1;
        res += query3(L, R, x, mid, left(node));
        res += query3(L, R,mid+1, y, right(node));
        return res;
    }
    
    // 在进行查询4的时候，由于左右儿子都可能只有一部分与查询区间相交，
    // 所有需要一个结构体来存储相交部分的相关信息。
    private class Ans {
        public int LLen = 0;
        public int RLen = 0;
        public int MLen = 0;
        public Ans() {}
        public Ans(int LLen, int RLen, int MLen) {
            this.LLen = LLen;
            this.RLen = RLen;
            this.MLen = MLen;
        }
    }

    public int query4(int L, int R, int x, int y, int node) {
        return query4Helper(L, R, x, y, node).MLen;
    }

    private Ans query4Helper(int L, int R, int x, int y, int node) {
        if ( y < L || x > R ) {
            return new Ans();
        }
        if (L <= x && y <= R) {
            return new Ans(LLen[node], RLen[node], MLen[node]);
        }
        lazyDown(node, y - x + 1);
        int res1 = 0, res2 = 0, res3 = 0, mid = (x + y) >> 1;
        Ans ans1 = query4Helper(L, R, x, mid, left(node));
        Ans ans2 = query4Helper(L, R, mid+1, y, right(node));
        res1 = ans1.LLen == (mid - x + 1) ? ans1.LLen + ans2.LLen : ans1.LLen;
        res2 = ans2.RLen == (y - mid) ? ans2.RLen + ans1.RLen : ans2.RLen;
        res3 = Math.max(ans1.MLen, ans2.MLen);
        res3 = Math.max(res3, ans1.RLen + ans2.LLen);
        return new Ans(res1, res2, res3);
    }

    private int left(int idx) {
        return idx << 1;
    }

    private int right(int idx) {
        return (idx << 1) + 1;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int T = sc.nextInt();
        for (int k = 0; k < T; k++) {
            int n, m, t, x, y;
            n = sc.nextInt();
            m = sc.nextInt();
            int[] arr = new int[n];
            for (int i = 0; i < n; i++) {
                arr[i] = sc.nextInt();
            }
            HDU3397 hdu = new HDU3397(n, arr);
            for (int i = 0; i < m; i++) {
                t = sc.nextInt();
                x = sc.nextInt();
                y = sc.nextInt();
                if (t == 3) {
                    System.out.println(hdu.query3(x, y, 0, n - 1, 1));
                } else if (t == 4) {
                    System.out.println(hdu.query4(x, y, 0, n - 1, 1));
                } else {
                    hdu.update(t, x, y, 0, n - 1, 1);
                }
            }
        }
    }
}

代码比较基础，速度与使用空间都不怎么样，但是至少AC了：

image

总结

线段树有很多不同的形式，而且很多时候根据题目的不同会有很多的小变化。

最重要的是代码一般较长，逻辑一般较乱，所有很容易出BUG，建议保持好心态。