线段树代码形式
1 | class SegmentTree { |
可以看到,通常线段树输入一个数组,同时维护自身的一个table数组。
提供query方法来完成对一个区间$[left, right]$的查询操作(最大值、最小值、求和等),
提供update方法来完成对输入数组某一位置的修改。
比如对于子数组最大值的查询,假设数组长度为$N$,查询$M$次,那么暴力方法查询的复杂度就为$O(MN)$, 而使用线段树则可以将每次查询的复杂度降到$log(n)$,那么总的复杂度就能降到$O(Mlog(N))$。
所以在某些时候,线段树是一个十分有用的数据结构。
线段树结构形式
树的性质
线段树其实就是一颗满二叉树,注意到这是一个十分重要的性质(使得可以使用数组快速建树), 它可以推出“假设叶节点个数为$n$,那么非叶节点的个数一定是 $n - 1$ ”, 那么同时也就表明总的节点数为 $n + (n - 1) = 2n - 1$ ,总的节点个数一定是奇数。
(这里使用的满二叉树定义为:除了叶子结点之外的每一个结点都有两个孩子结点。)
下面可以简单的证明一下推论“假设叶节点个数为$n$,那么非叶节点的个数一定是 $n - 1$ ”:
- 假设总结点树为$n$,非叶节点数为$n_1$,叶节点数为$n_2$,那么$n = n_1 + n_2$。
- 由二叉树的性质,分支数(边数)为$n - 1$。
- 由非叶节点都有两个儿子,分支数(边数)也可以计算为$2n_1$。
那么:
可以推出:
推论得证。
线段树数据结构
线段树通常使用一个数组T来进行存储,根节点在T[1]的位置(T[0]不使用),
一个节点T[i]的左儿子为T[2i],右儿子为T[2i+1],父节点为T[i/2]。
对于最大值来说,每个节点维护以这个节点为根的子树的最大值,所有输入的数据都存放在叶节点。
建树:
复杂度:$O(n)$
1 | class SegmentTreeMax { |
建树时就使用了上面的性质:假设叶节点个数为$n$,那么非叶节点的个数一定是 $n - 1$ 。所以这里直接申请一个2n大小的数组,
然后从1到n-1为作为非叶节点,n到2n-1作为叶节点。
对于[1, 2, 3, 4, 5, 6]来说,它建立的数组为[0, 6, 6, 2, 4, 6, 1, 2, 3, 4, 5, 6](注意索引0不使用),形状为:
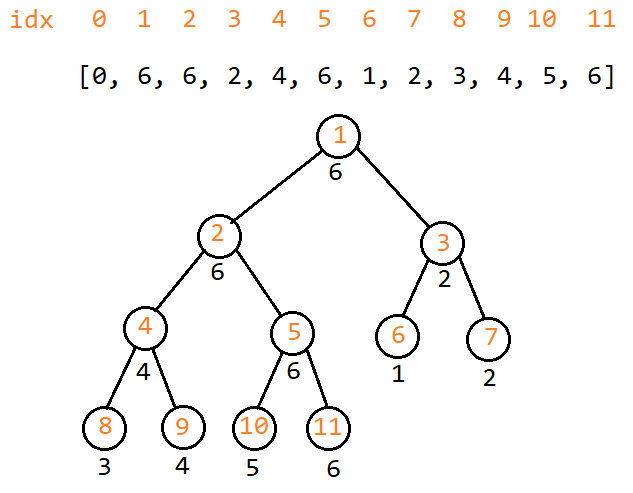
更新:
复杂度:$O(log(n))$
更新很简单,更新叶节点后再迭代更新父节点即可:
1
2
3
4
5
6
7
8
9
public void update(int idx, int num) {
idx += n;
table[idx] = num;
idx = parent(idx);
while (idx > 0) {
table[idx] = Math.max(table[left(idx)], table[right(idx)]);
idx = parent(idx);
}
}
1 | public void update(int idx, int num) { |
线段树的查询
复杂度:$O(log(n))$
线段树的查询才是线段树的精髓所在,其实二叉树这种分治的思想并不是一个难以想到的方法, 但是分治后的子问题结果的合并才是这里比较重要的地方。
线段树的结构已经将问题划分到了一个个子树之上,但是在进行区间查询时,区间可能跨越多颗子树:
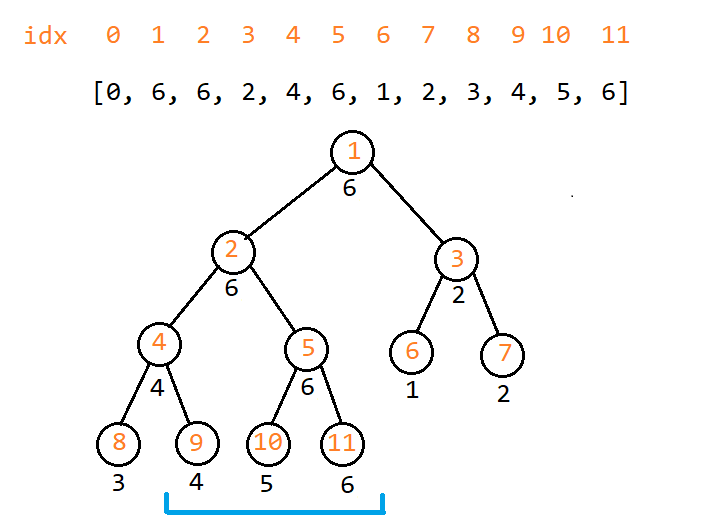
例如上图,它查询原数组中[3, 5]区间(树中的节点9、10、11)中的最大元素,很明显的,9号节点单独在一颗子树之中。
首先需要注意到上面线段树数据结构中所说“一个节点T[i]的左儿子为T[2i],右儿子为T[2i+1]”,
那么所有左儿子的节点序号都是偶数,而右儿子的节点序号则都是奇数。
那么对于一个查询区间[L, R](L不等于R):
- 对于区间的左边界L,如果它是偶数,那么它是父节点的左儿子,那么它的兄弟节点L+1(父节点的右儿子)也属于这个区间之内,那么对于最大值,应该直接向上询问它的父节点。
- 对于区间的左边界L,如果它是奇数,那么它是父节点的右儿子,那么它的兄弟节点L-1(父节点的左儿子)肯定不属于这个区间之内,那么对于最大值,直接询问节点l,不能向上询问它的父节点。
对应以上结论:
- 当左边界L为偶数时:
L = parent(L)。 - 当左边界L为奇数时:
max = Math.max(max, L)。这里完成了对L这个点的查询,那么就可以对区间进行缩小,即:L = L + 1(注意到L变成了偶数)。
右边界的处理同理左边界。
可以看到这是一个不断收缩区间左右边界的过程,并从叶节点逐渐向上走,实际代码如下:
1 | public int query(int l, int r) { |
代码在不断缩小区间的过程中,并且对于更新后的L'、R',能够保证 $[L’, R’] \in [L, R]$ ,也不会遗漏任何区间内的元素。
线段树代码
区间最大值:
1 | class SegmentTreeMax { |
上面是基本的代码形式,可以依据它来修改为各种不同的用途。
Leetcode 1157
题目大意是给定一个数组,提供以下功能:
- 查询一个区间内的
majority-element,也就是这个数的出现次数大于给定的threshold,注意threshold一定大于这个区间的一半大小, 这样即能保证一个区间里面最多只存在一个majority-element。
注意到这个题目最关键的思想点在于:
一个区间(区间大小N)中的一个数A,它在区间内的出现次数大于N/2,那么无论将这个区间切分为几个小区间,
这些小区间中,必定至少存在一个小区间t(区间大小n),A在小区间t中的出现次数大于n/2。
这个证明使用反证即可:
假设区间$T$,大小为$N$,其中数$A$出现次数$A_T$大于$\frac{N}{2}$。
现在将区间$T$划分为小区间$\{ T_1, T_2, T_3, … , T_m \}$,区间大小为$\{ n_1, n_2, n_3, … , n_m \}$,$A$的出现次数为:
如果所有的小区间中,A的出现都不到区间的一半:
那么:
显然与假设中的 $A_T$大于$\frac{N}{2}$ 相矛盾。
一旦想通了这个Punchline,就可以开始使用线段树来做这个题了,线段树中每个节点存储以它为根的子树中最多的元素, 那么一个区间内的最多的元素,就类似于求这个区间内的最大元素,只不过最大元素比的是大小,而这里比的是在子区间中出现的次数多少。
注意到一个查询区间可能由多个子树组成,这就类似与多个子区间,那么这个majority-element一定会出现在某课子树的根节点上。
当然这里还有另一个重点:如何快速查询一个数在一个子区间内出现多少次?如果使用遍历,那么是$O(n)$的复杂度。
一个巧妙的方法是将这个数的所有索引存下来形成一个List,通过二分查找来查询子区间的左右边界在List中出现的位置, 相减即可知道子区间中这个数的数量,复杂度$O(log(n))$。
最后代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
class MajorityChecker {
private int[] table;
private Map<Integer, List<Integer>> numIdxs = new HashMap<>();
private int n;
public MajorityChecker(int[] arr) {
this.n = arr.length;
table = new int[n*2];
for (int i = n, j = 0; i < table.length; i++, j++) {
table[i] = arr[j];
List<Integer> idxs = numIdxs.get(arr[j]);
if ( idxs == null ) {
idxs = new ArrayList<>();
numIdxs.put(arr[j], idxs);
}
idxs.add(i);
}
for (int i = n-1; i > 0; i--) {
int l = left(i), r = right(i);
table[i] = countRange(l, r, table[l]) > countRange(l, r, table[r]) ? table[l] : table[r];
}
}
private int countRange(int l, int r, int num) {
List<Integer> idxs = numIdxs.get(num);
int idx1 = Collections.binarySearch(idxs, l);
int idx2 = Collections.binarySearch(idxs, r);
if (idx1 < 0) {
idx1 = -(idx1 + 1);
}
if (idx2 < 0) {
idx2 = -(idx2 + 1) - 1;
}
return idx2 - idx1 + 1;
}
public int query(int l, int r, int threshold) {
l += n;
r += n;
int ll = l, rr = r;
int res = 0;
int max = 0;
while ( l <= r ) {
if ( (l & 1) == 1 ) {
int tmp = countRange(ll, rr, table[l]);
if (tmp > max) {
max = tmp;
res = table[l];
}
l++;
}
if ( (r & 1) != 1 ) {
int tmp = countRange(ll, rr, table[r]);
if (tmp > max) {
max = tmp;
res = table[r];
}
r--;
}
l >>= 1;
r >>= 1;
}
return max >= threshold ? res : -1;
}
private int left(int idx) {
return idx << 1;
}
private int right(int idx) {
return (idx << 1) + 1;
}
}
1 | class MajorityChecker { |