总结一下自己2018年参见华为软挑的心里历程吧。
自己连续两年参加华为软挑,都止步于区域复赛,去年第9,今年第10。
第一年水平不够,第二年时间不够(当然主要是自己水平不够),也是有一点遗憾吧。 当然,自己参赛的目标就是进入复赛,所以也还好了。
下面内容分为初赛和复赛,但是预测部分单独拿出来,因为它前后的思路没有太大变化。
初赛
比赛题目
由于租户对ECS实例(虚拟机,VM)请求的行为具有一定规律,可以通过对历史ECS实例请求的分析,预测到未来一段时间的ECS实例请求,然后对预测的请求分配资源,这样可以 找到一个接近最优的分配策略,实现资源最大化利用,同时也能参考预测的结果制定云数据中心的建设计划。
赛题分为两个部分,一个是虚拟机数量预测,一个是虚拟机最优化部署。
具体来说就是:
- 一个数据中心的场景。
- 数据中心现在的业务是向客户出租虚拟机。
- 客户有多种规格的虚拟机可以选择。
- 出租虚拟机有一定的规律。
- 如果能够预测到未来一段时间需要出租的虚拟机,就可以提前针对进行部署。
上面就是虚拟机数量预测的部分。
部署部分:
- 有一堆虚拟机(多种不同规格)需要部署。
- 有不同规格的物理机提供挑选,使用数量没有限制。
- 主要考量两个资源维度,CPU以及内存。
- 假如考量的是CPU,那么,利用率为
虚拟机总CPU / 使用的物理机总CPU。
这一部分就是最优化部署部分。
虚拟机规格:(题目中定死)
1 | flavor1 1 1024 |
输入样例,分为train.txt和input.txt:
train.txt:
1 | 565f3813-9c5f flavor6 2015-12-01 00:17:03 |
每一行就是在某个时间,有客户在某个时间租借了某个规格的虚拟机。
注意,可能规格会出现flavor20等情况,需自行处理。
input.txt:
1 | 56 128 1200 |
第一行表示物理机的规格(CPU 内存 硬盘),当然硬盘在本次比赛中就不需要考虑。
第二部分是需要预测的虚拟机,主要信息是哪几种规格的虚拟机需要预测,后面带的是虚拟机的cpu和内存(MB), 当然,这个规格信息也是多余的,因为这都是题目固定的规格。
这里的CPU就代表部署时考量CPU。
最后两个日期是需要预测的时间段。(一定会挨着最后的历史数据日期,时间段小于两周)
输出样例,:
1 | 6 |
第一部分,一共6台虚拟机,需要预测的规格每种各是多少(为0也要写)。
第二部分,使用4台物理机,怎么放。
评分公式:

也就是预测部分要准确,部署部分最优化,才能达到比较高的分数。
部署部分思路
先说部署部分,这一部分比较好说一点。
先看公式,利用率为虚拟机总CPU / 使用的物理机总CPU。
- 在预测完毕之后,实际上虚拟机的数量和规格都确定了,那么分子实际上就确定了。
- 分母的大小和使用物理机总数有关。
看上面两点可以发现,真正的目标其实是使用最少的物理机来进行部署,和分子大小无关, 所以究竟是考虑CPU还是内存,其实都是一样的优化目标,解出来的答案都是一样的。
那么,这个问题就变成了有一堆东西需要用背包装,使用背包个数越少越好,一想就是个背包问题, 当然,背包问题是问一个背包能装多少东西,这里是使用最少的背包来装东西,所以还是不太一样。
这里实际上应该是一个装箱问题,瞬间变成了一个NP难问题,只能使用近似解法来求解。
首先,第一种启发式解法就是,使用一个背包,尽量装满,然后换下一个背包,这里就把它叫做贪心背包。
然后参考:装箱问题近似算法概述
那么这里的解法就有:
- 贪心背包。
- 降序首次适应算法(FFD, First Fit Decreasing)。
- 降序最佳适应算法(BFD, Best Fit Decreasing)。
- 升序首次适应算法(FFI, First Fit Increasing)。
- 升序最佳适应算法(BFI, Best Fit Iecreasing)。
而且这里的value值可以使用CPU,也可以使用内存,所以相当于一共有10种不同解法。
那么如何选择呢?当然是不选择,这些算法的运行速度都非常快,直接将它们全部用一遍,使用最好的那一个。
trick:
如果最后一台物理机只装了一个很小虚拟机,但是这已经是算法解出来最好的方式了,但是它拉低了总的利用率,怎么办?那么这里直接将这个虚拟机删除了就得了, 也就是对预测进行微小的修改。由于预测本来就不是很准,小修改并不会带来什么影响,但是能提升利用率。
复赛
题目变化
复赛题目相比较初赛,只有一些小的变化。
- 初赛物理机规格只有一种,这里变为三种。
- 部署同时考量CPU和内存。
- 预测时间段变为1~4星期,并且可能从训练数据结束后0~2星期内开始。
- 需要预测的虚拟机规格增加到18种。
部署上的变化
这里由于多了两种规格的物理机,而且同时考量的CPU和内存,所以这里就需要有所变化。
这里的优化目标相当于最小化剩余资源的碎片大小,考虑贪心背包方法,这里背包的value值就需要重新定义,
为了达到最小化剩余资源的碎片大小的目标,试着把一种规格的虚拟机value定义为:
虚拟机CPU/物理机CPU + 虚拟机内存/物理机内存
那么这里有三种规格的物理机,怎么选呢?在使用一个新背包来装的时候,将三个背包都试一遍,选择装的最满的那一个。
这个最满的定义就是碎片率最小,物理机使用CPU/物理机CPU + 物理机使用内存/物理机内存。
结果这里的效果非常好,基本能够达到部署分数97%以上…启发式有时候就是这样。
PS:
程序里面在两台物理机一样满的时候,还使用了一种奇葩的比较方式,而且思路上是写错了才出现的,结果效果更好了…
由于代码写错了导致看不懂思路,这里没法阐述…
总之通过这样的方法,在部署问题上的提升空间不大了。
预测部分
其实就像上面部署所描述的,虽然部署是个NP难问题,但是其实部署很多时候都能接近最优或者是达到最优, 所以最难的部分还是在预测上面。
分析数据
比赛给了一部分线下训练数据,当然只是用来进行线下的测试,测试现在的预测模型的效果,而不是用来训练模型, 因为这次比赛的训练阶段是放在线上进行的,会输入训练数据。而且线下的这部分训练数据并不多。
而且数据很奇怪,分成两个部分,2015.01~2015.08和2015.12~2015.01,这就导致第二部分的数据时间段较短,
并且与第一部分的数据差距很大。
这里为了连续性,所以只分析了2015.01~2015.08这一块数据。
总体分布:
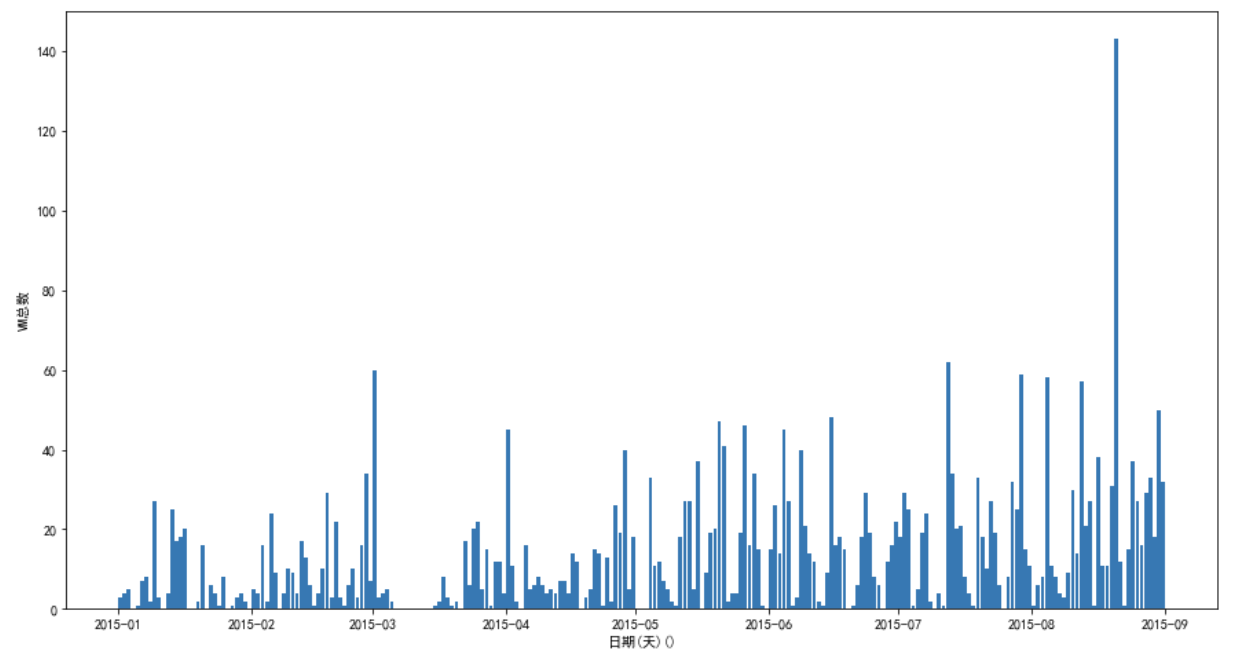
可以看到每一天的VM数量都有很大的变化,看不出有什么规律。
每周的VM数量:
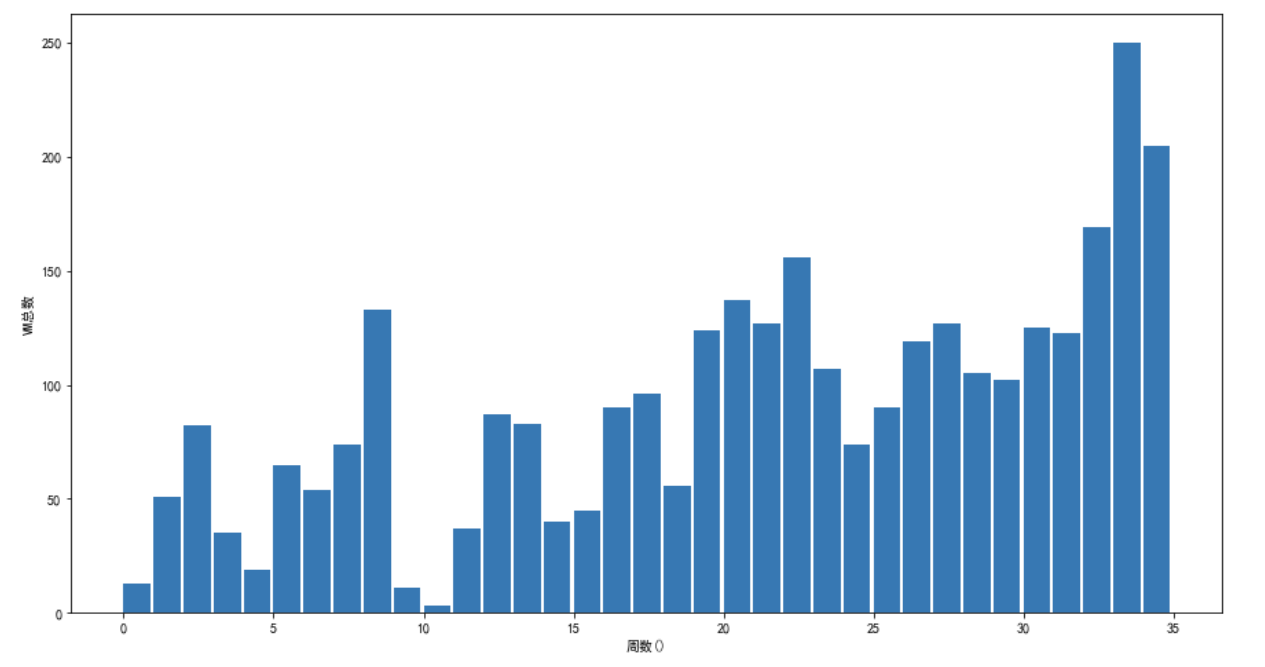
这个可以明显的感觉到后面的VM数量比前面的要多。
VM数量累计和:
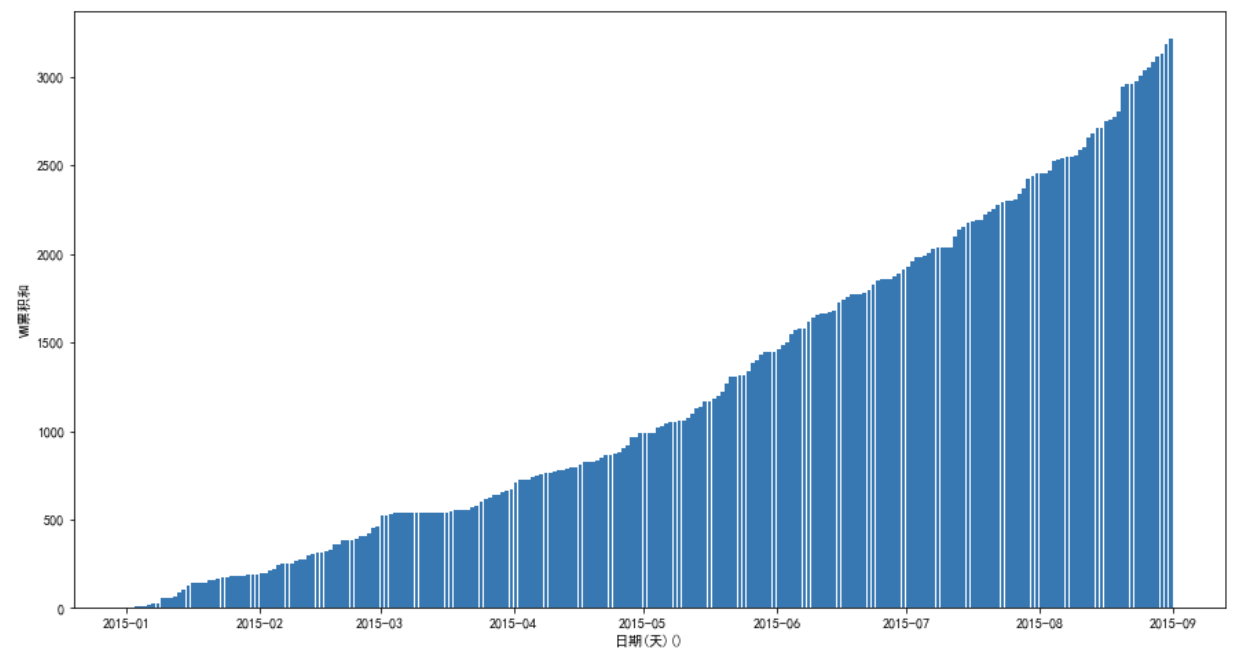
上面的图看着就比较平滑,有一点线性增长的感觉,当然图上略微比线性增长快一点。
下面分布画出几种flavor的数据分布情况。
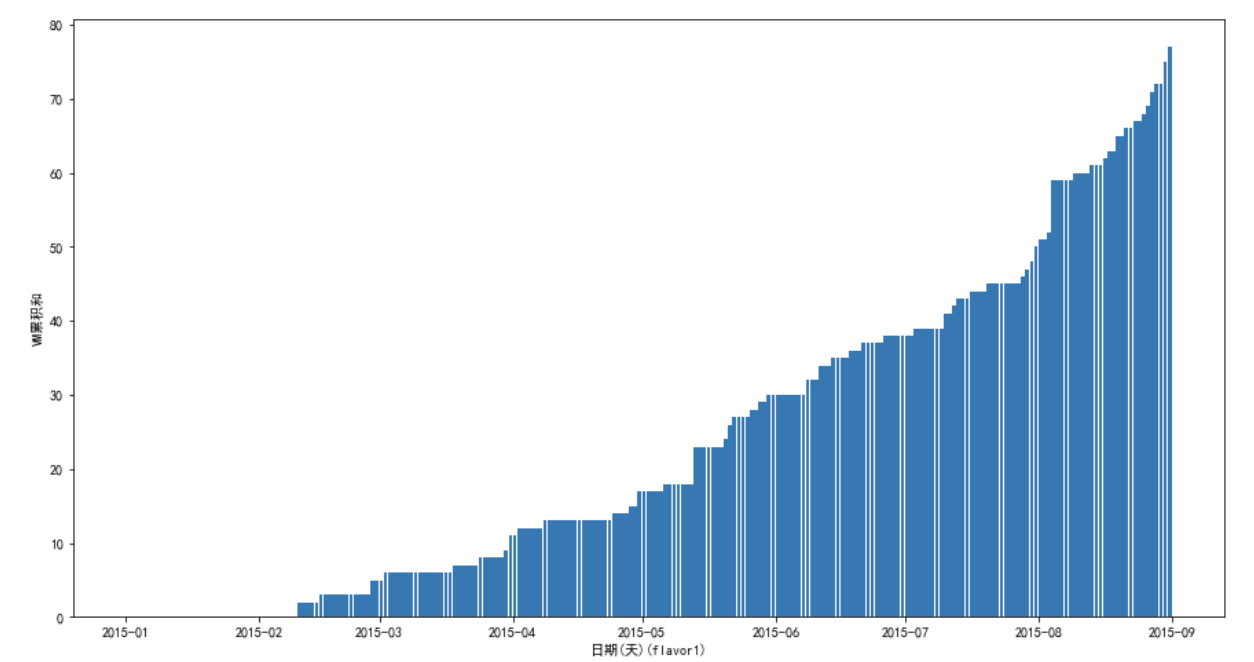
flavor1:
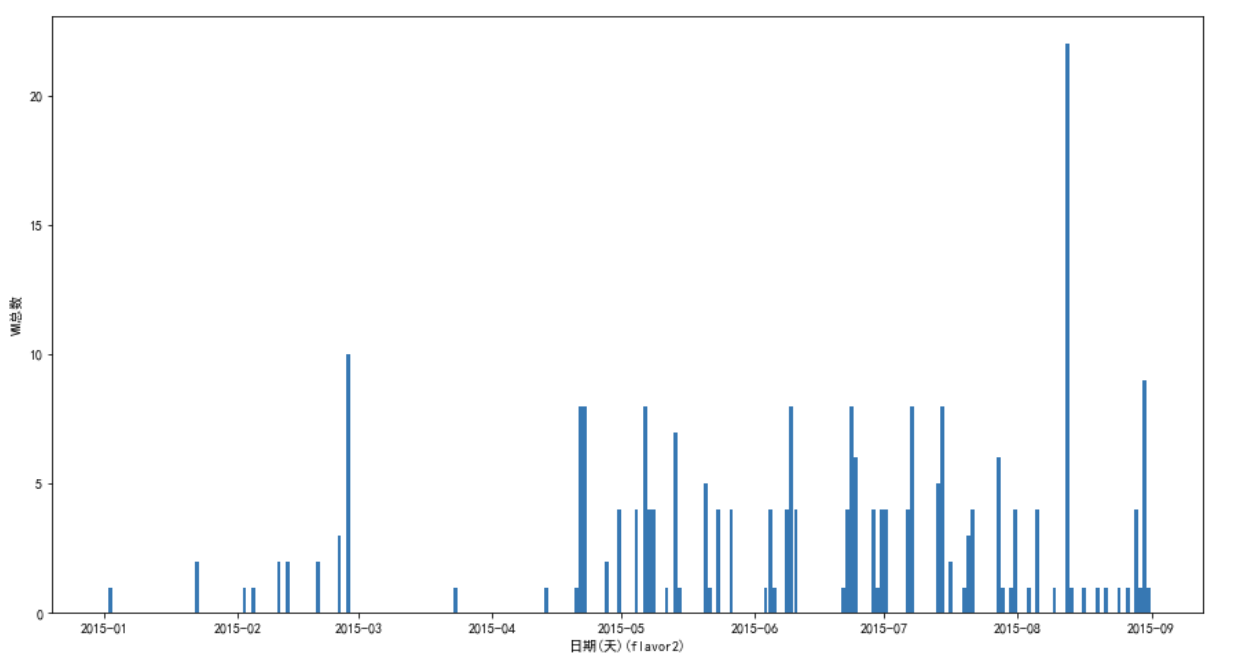
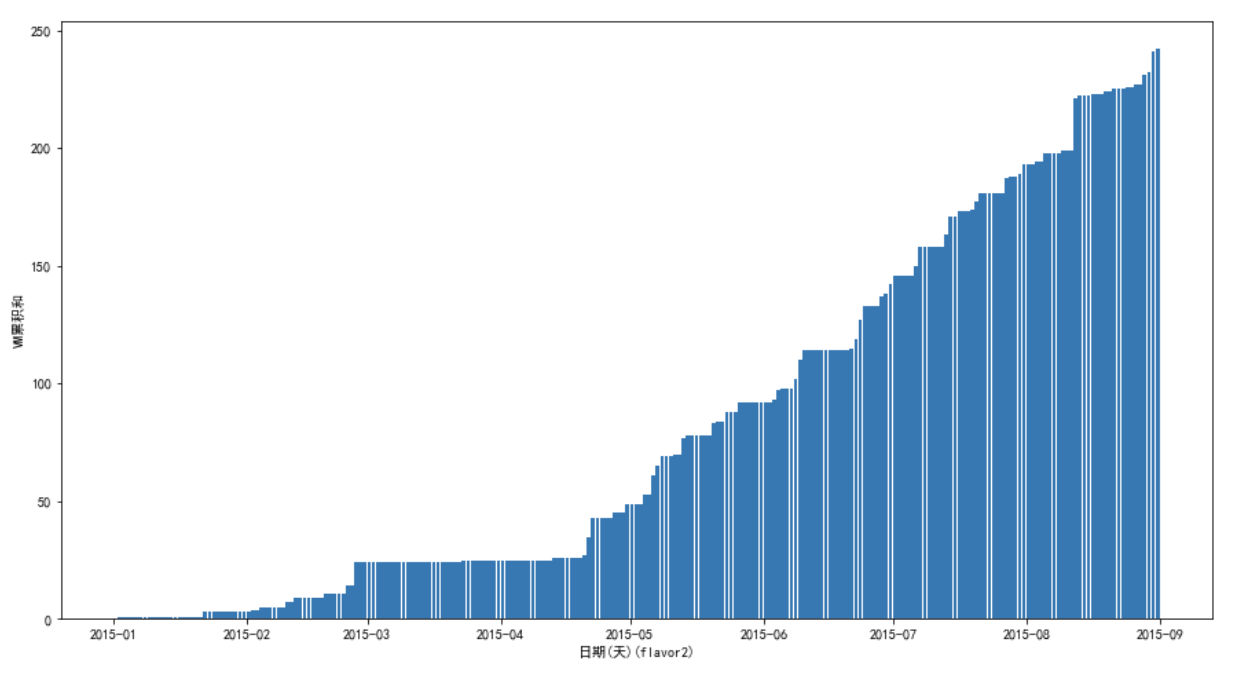
flavor2:
flavor8:
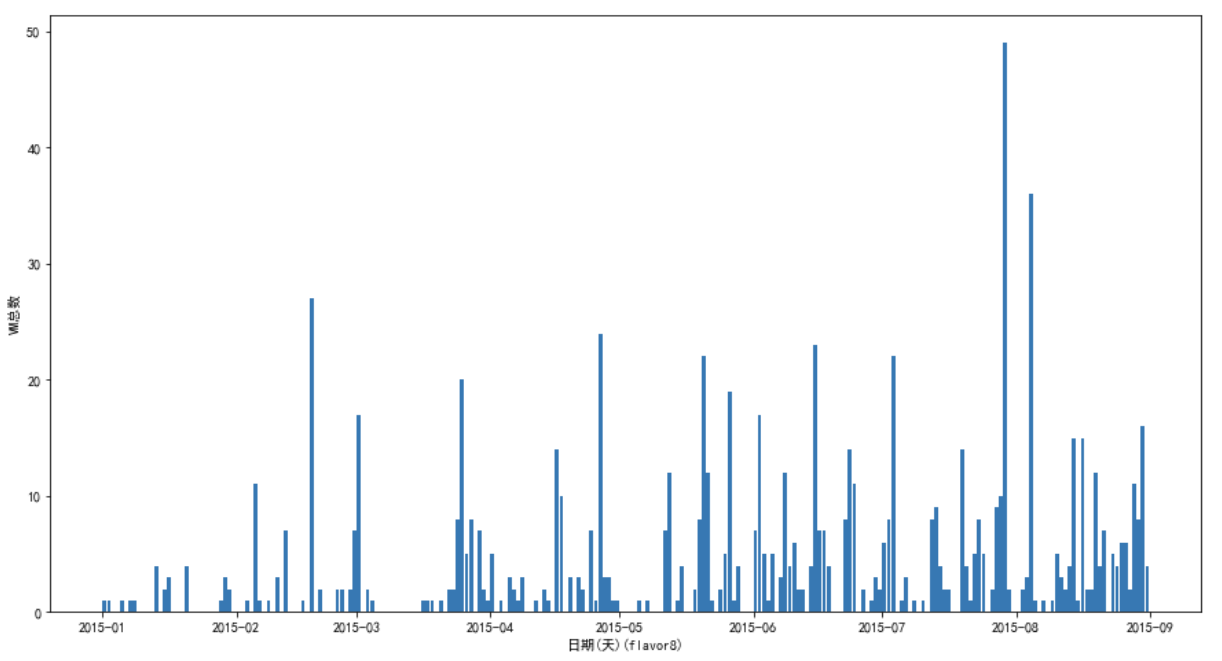
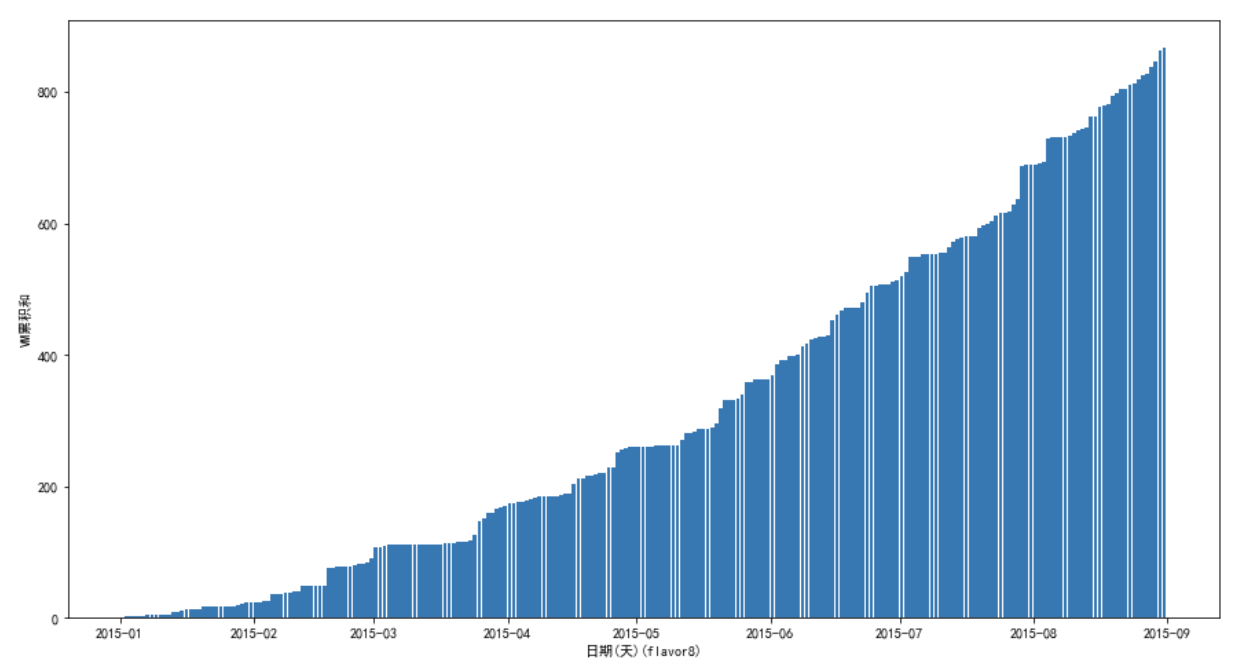
上面没有把所有都画出来,但是实际上差不多,可以发现数量分布很不均匀,有的flavor数量多, 画图看起来就比较平滑,有的flavor数量少,看起来很难看。
这也导致了模型很难达到较高的精度,因为数据本来就带有了太多的随机性。
基本模型思路
这里首先就会想到使用线性回归,当然,这里的线性回归可能有两种理解,
线性回归理解1:
样本有n个属性,通过n个属性乘上n个权重相加得到y。
那么可以把前面n天的VM数量作为样本属性,后面接着一段时间的vm数量作为样本y,来进行模型训练。
线性回归理解2:
就是一条直线,
那么也就是 x 就是某一天(或者某段时间), y就是这一天(或这段时间)的VM数量。
这里为了简单,我把线性回归理解2叫做真线性回归。
这里当然还可以使用别的模型,例如,
二次函数回归:
这个就类似真线性回归,只不过使用二次曲线来拟合。
LSTM:
这种时间序列的肯定会想到LSTM,但是这里数据量太少,直接PASS。
神经网络:
同样的这里数据量太少,直接PASS。
arima:
写起来可能比较复杂,而且效果可能也不会好,感觉这里数据没太多内在规律,数量量也不够。 究竟怎么样,这里没有尝试,不得而知。
直接平均法:
直接使用平均算出每一天或者每一周一种VM的数量,实际上效果还行。
加权平均法:
和平均的思想一样,但是越往后的天数权重越大,因为间隔时间越近的数据之间相关性肯定是越强。效果好于直接平均法。
直接(加权)平均乘系数法:
直接(加权)平均挺好的,但是通常结果偏小,因为VM增加越来越快,所以可以在直接平均的基础上再乘上一个大于1的系数。 事实上,大部分人使用的都是这个方法,系数完全靠猜。好吧,我们也是使用这样的方法进入复赛的。
基本采样思路
采样应该依据模型来进行,不同模型对于采样的要求不一样,对比线性回归和真线性回归, 它两之间对于采样就有不一样的要求。
还需要注意的是,从上面图就可以看出,采样以天为基本单位,效果可能很差,因为变化太大了。 而且,星期六与星期天的VM数量较少。
所以采样可以用周作为单位来采样。
时间段采样
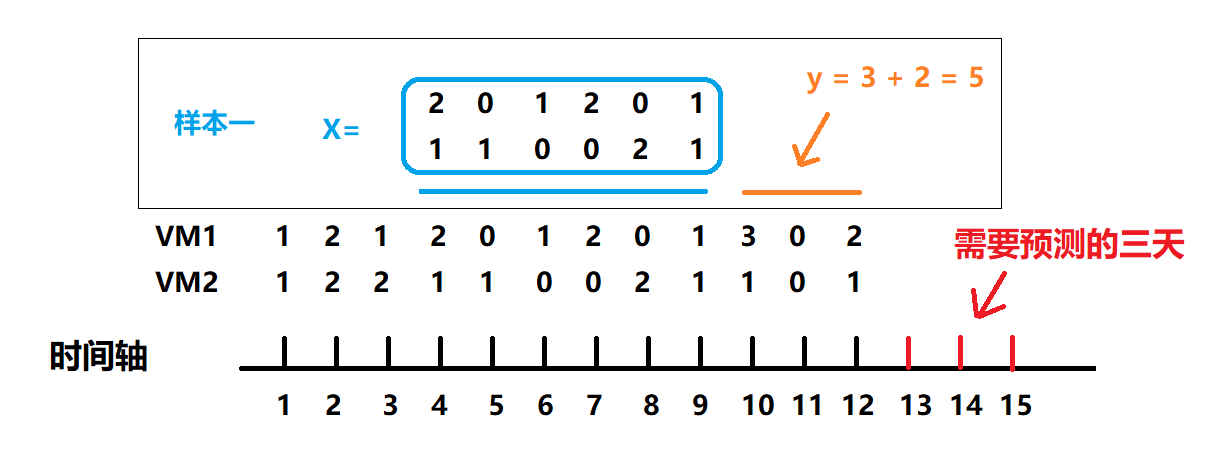
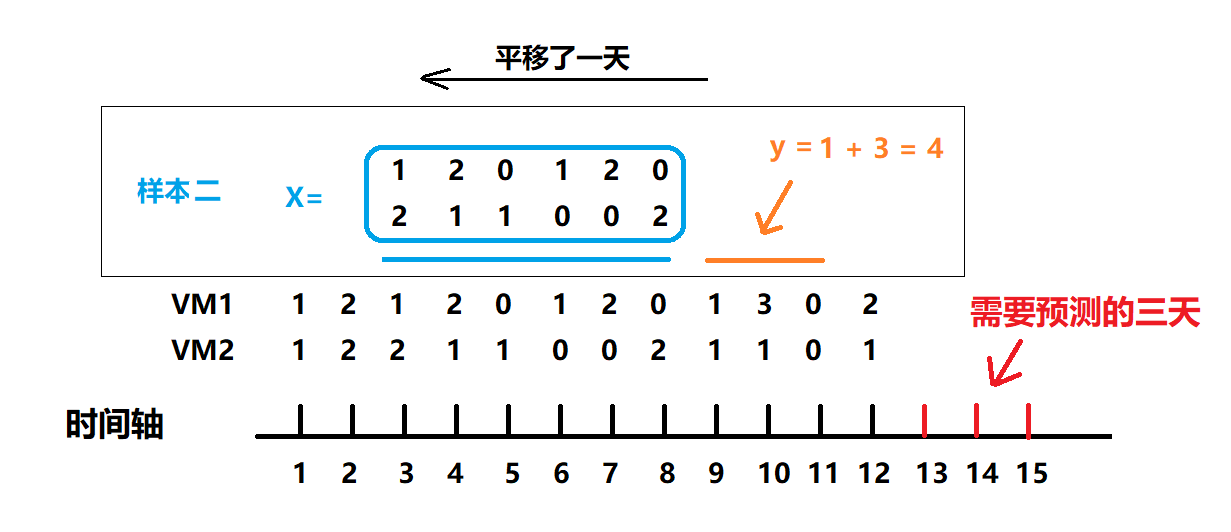
上图的采样方式以某几天作为X,后面几天作为Y,当然作为Y的这”几天”的长度一般设置为等于输入需要预测的时间段长度。
这里对每种VM的数量进行区分。
这样的采样方式得到的样本就比较适合线性回归、神经网络等模型。
图中X的某一列就是某一天VM的发生数量。这里为了平滑X的属性,可以将这一列的数值转化为以这一天为结束的前一周的VM总和。
按周采样
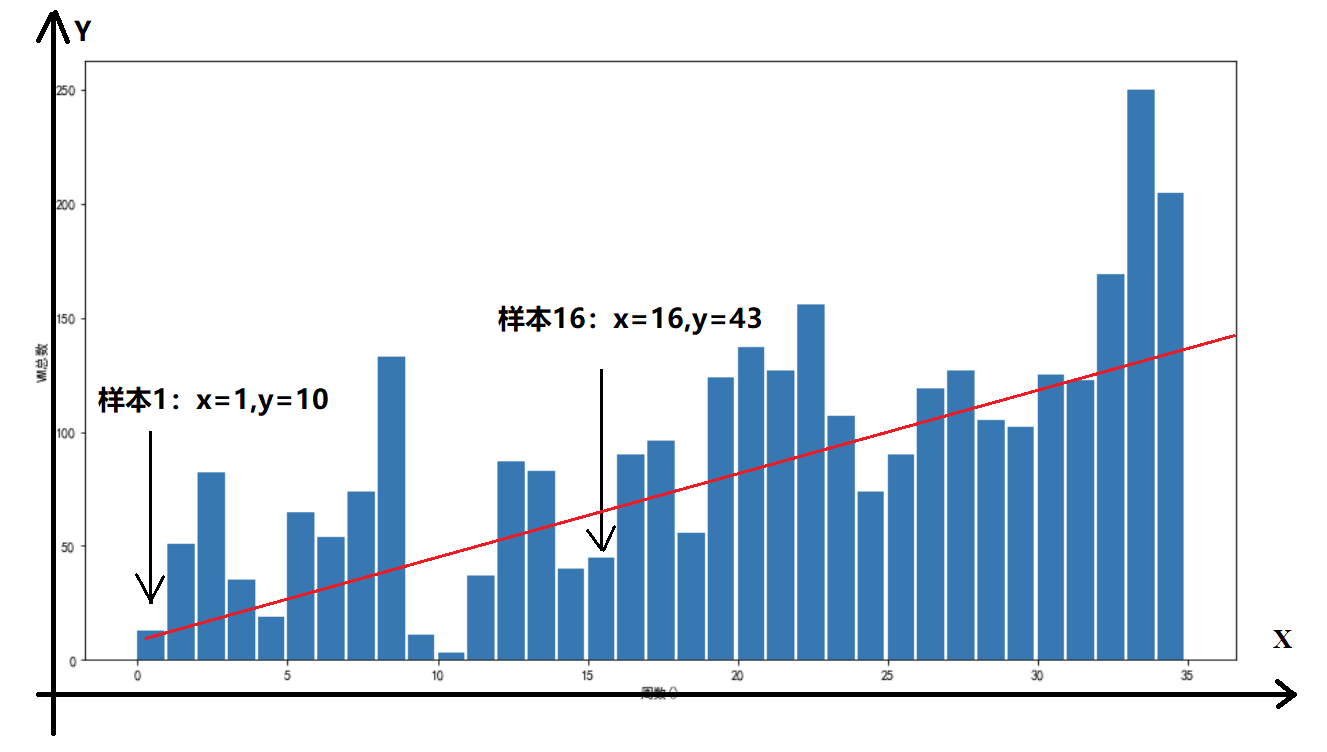
图中以每一周作为一个x坐标,这周的VM数量作为y。
这里对每种VM的数量进行区分。
这种采样方式就比较适合真线性回归,学习出来的直线就类似图中的红线。
VM总和采样
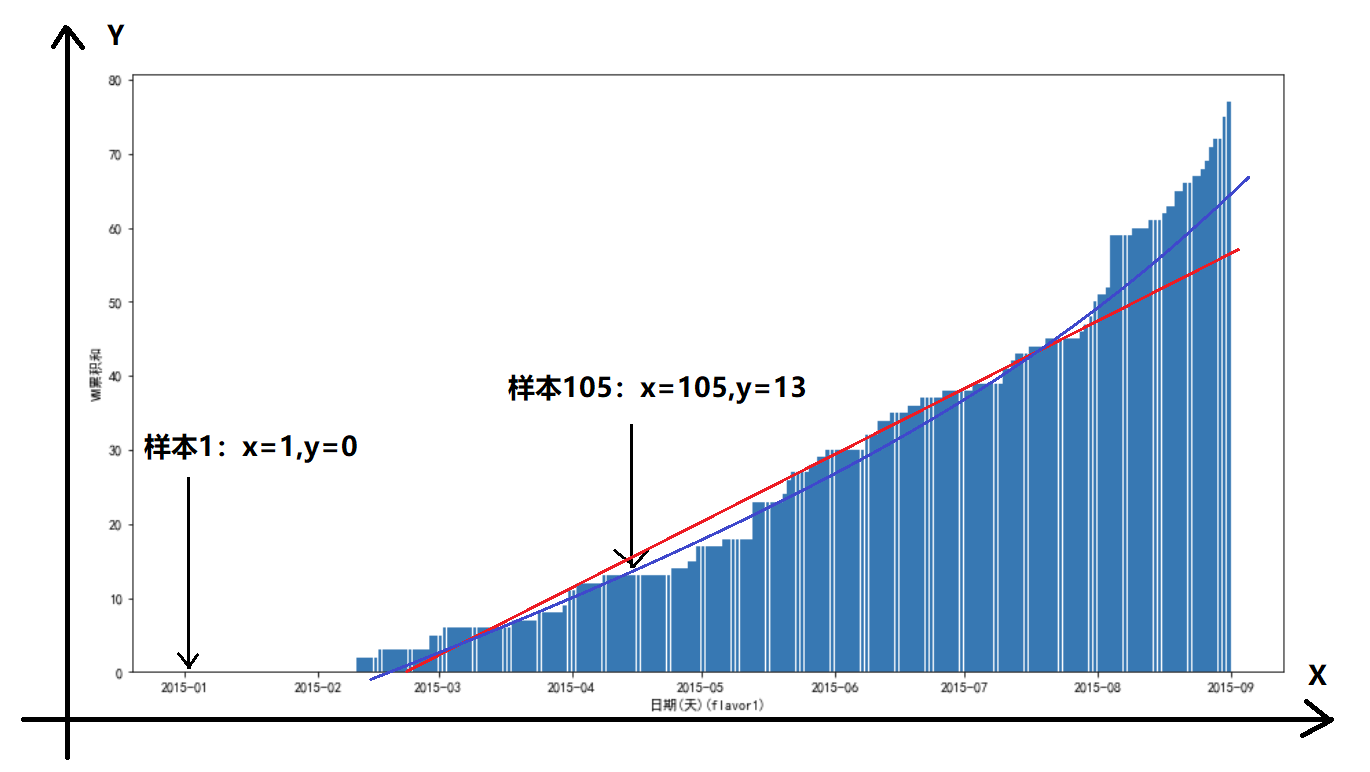
这里的采样以每一天为一个单位,但是这里的y表示从开始到这一天,flavor数量的累计。
这里对每种VM的数量进行区分。
这样采样的目的是为了使得样本更加平滑,适合真线性回归模型。
图上的红线就是真线性回归,蓝线就是二次回归。
不区分VM的种类
上面的采样都是对VM的种类进行了区分的,这里还有一种思路,就是不对VM的种类进行区分, 采样直接针对所有VM的数量之和。
那么这样学习出来的模型只能预测出所有种类的VM总量,但是题目需要的是某一种VM的数量, 怎么办?
这里可以通过历史数据,统计每一种VM所占总量的百分比,然后将预测出来的结果乘上相应比例,得到对于VM的数量。
这样不区分VM的种类的好处,就是能使得数量变化更加平滑,真线性回归能有更好的学习效果。
PS:
这里进行模型学习的时候,使用的都是随机梯度下降(SGD),当然,对于真线性回归来说,可以直接使用直接求解得到最优解, 但是这里没有使用,因为试了一下效果反而变差了,不知道为什么。
最终提交模型
初赛如上面所说,使用的是加权平均乘系数法。
在复赛中,尝试了几种模型,包括加权平均法乘系数,效果都不好。
最后一次提交的模型效果好一点,要不连第10名都没有,这个模型是:
不区分VM的总和采样 + 真线性回归 + 直接平均法 + 只使用最近两个月的数据
这里对于占总量的比例大于0.02的VM,使用真线性回归得到的预测结果,但是对于小于0.02的VM,
使用的是直接平均法。对于离得太远的数据,使用之后反而会使得效果变差,所以通常都不会把所有的训练数据都用上。
最后只得到了第10名,很遗憾没有进入复赛。
有空再看看别人的博客吧。