SFC分配简单实验

github链接

2017年11月17日

生成数据集

这里先固定好整个SFC的结构，也就是一共几类VNF，以及每一类SFC的实例个数，以及QOS属性的数量和前向属性的个数K。

可以变动的参数有：

• 每一个VNF当前的QOS取值
• 每一个属性的权重

---

那么生成的样本的输入属性就是:所有VNF当前的QOS，以及每一个属性的权重组成的一个向量

样本的标签为每一类VNF的选择。

---

模拟环境示意图

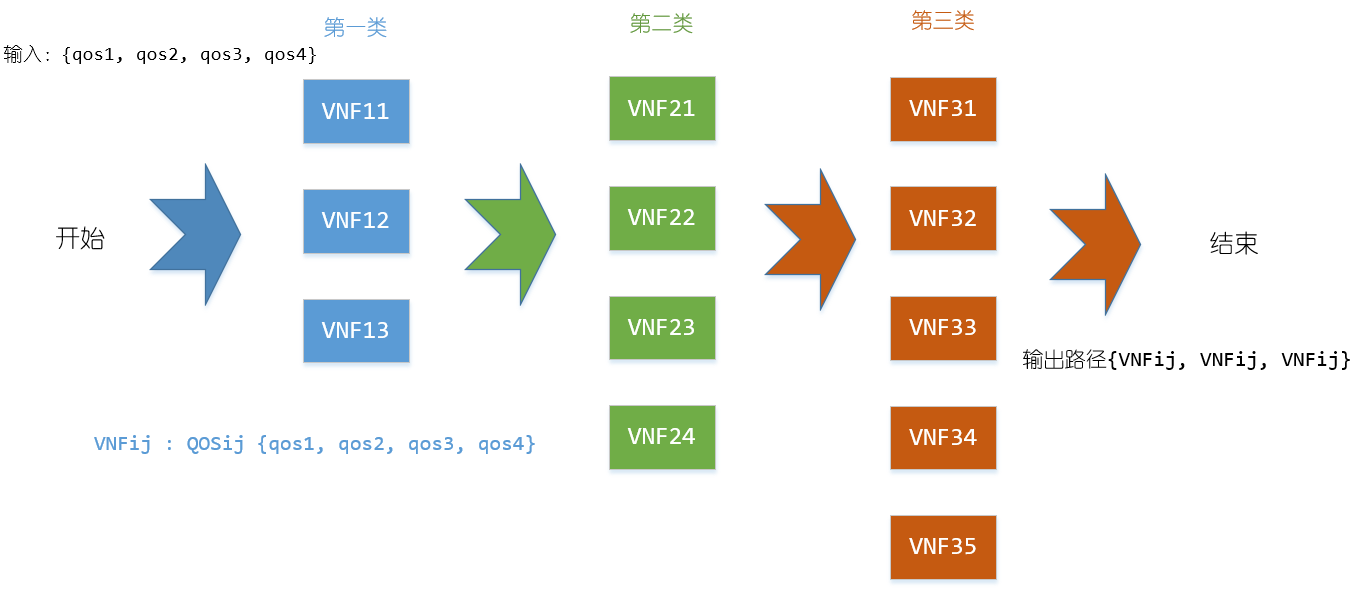
确定到网络的结构

__init__(self, num_i = [2, 3], scope_L = [[1, 1000],[1, 100]], K = 1)

num_i为每一类VNF的数量

scope_L 为每一个QOS属性的取值范围

K 为前向属性的数量

随机QOS请求

首先确定出QOS请求的范围

注意到应该有QOS不能被SFC所满足

那么这里将它的范围上限定义为属性的上限乘上VNF的种类数，下限就为属性的下限。？

生成样本写入文件

生成一百万条样本

写成CSV文件

import numpy as np
import sfc_model as sfc

num_i = [3,4,5]

scope_L = [[1, 1000],[1, 100],[1,100],[1,1000]]

K = 2

my_model = sfc.sfc_model(num_i = num_i, scope_L = scope_L, K = K)

def random_qos( N = 3, scope_L = [[1, 1000],[1, 100],[1,100],[1,1000]], K = 2 ):
    L = len(scope_L)
    qos = np.zeros(L)
    for i in range(L):
        qos[i] = np.random.rand(1)[0] * (scope_L[i][1] * N - scope_L[i][0]) + scope_L[i][0]
#         if i < K:
#             qos[i] = np.random.rand(1)[0] * (scope_L[i][1] * N - scope_L[i][0]) + scope_L[i][0]
#         else:
#             qos[i] = np.random.rand(1)[0] * (scope_L[i][1] * N - scope_L[i][0]) + scope_L[i][0]
    
    return qos

## 把 path 变成一个分类问题

N = 3
back_muti = np.zeros(N)
category = 1
for i in range(N):
    back_muti[i] = 1
    category = category * num_i[i]
    for j in range(i+1, N):
        back_muti[i] = back_muti[i] * num_i[j]

def get_category(path):
    if path is None:
        return category
    
    cate = 0
    for i in range(N):
        cate = cate + path[i] * back_muti[i]
    
    return int(cate)

T = 100 
N = 3
num_i = [3,4,5]
samples = np.zeros((T, len(scope_L)*np.sum(num_i) + len(scope_L)*2))
# labels = np.zeros((T, len(num_i) + np.sum(num_i)))
labels = np.zeros((T, category+1))
for t in range(T):
    qos = random_qos()
    my_model.construct()
    path, _ = my_model.serveQOS(random_qos())
    sample = qos
    sample = np.hstack((sample, my_model.W))
    sample = np.hstack((sample, my_model.qoses.reshape(-1)))
    label = np.zeros(category+1)
    idx = get_category(path)
    label[idx] = 1          
    samples[t] = sample.reshape(1,-1)
    labels[t] = label.reshape(1,-1)
    
    if t % 1000 == 0:
        print(t)

np.savetxt('data/X_train.csv', samples, delimiter = ',')
np.savetxt('data/Y_train.csv', labels, delimiter = ',')

神经网络

直接使用keras，使用一个三隐藏层的神经网络进行尝试。

每一层1000个神经元。

def my_net(input_len = (56,), output_len = 61):
    
    X_input = Input(input_len)
    X = Dense(1000, activation='relu', name='fc1', kernel_initializer = glorot_uniform())(X_input)
    X = BatchNormalization(name = 'bn1')(X)
    
    X = Dense(1000, activation='relu', name='fc2', kernel_initializer = glorot_uniform())(X)
    X = BatchNormalization(name = 'bn2')(X)
    
    X = Dense(1000, activation='relu', name='fc3', kernel_initializer = glorot_uniform())(X)
    X = BatchNormalization(name = 'bn3')(X)
    
    X = Dropout(0.7)(X)
    
    X = Dense(output_len, activation='softmax', name='output', kernel_initializer = glorot_uniform())(X)

    model = Model(inputs = X_input, outputs = X, name='DemoNet')
    
    return model

目前的效果

使用100万条样本，其中70万条作为训练集，30万作为测试集。

Epoch 50/50
 - 124s - loss: 1.0770 - acc: 0.6653
Test Loss = 1.12501473908
Test Accuracy = 0.668746666667

2017年11月24日

sfc网络数据生成

前提：

1. 网络结构最大5*5,否则网络过大会造成数据量爆炸。
2. Qos属性数量最大为4。理由同上。
3. 想象中，请求从前向后依次经过每一类VNF，因为这里是加性的权重，经过顺序其实没有关系。
4. Qos属性的取值范围确定。反正进行归一化之后，范围没有任何影响。

可变参数：

1. 网络中存在的VNF。在5*5的网络结构矩阵中，存在的VNF取值为1，否则为0。
2. VNF的Qos取值。由于是4维属性，那么就是5*5*4的矩阵。
3. 前后向属性的个数。前向属性，Qos取值乘上-1。
4. 每一个属性的权重。4维属性，那么将每一个属性的权重扩张为5*5的矩阵，组成5*5*4的矩阵。
5. Qos请求。4维属性，与上面相同，扩张为5*5*4的矩阵。

注意：这里的参数之所以设计为矩阵，是为了利用到卷积神经网络。

---

样本属性：

4层Qos属性取值，4层Qos属性权重，4层Qos请求，总共12层，5*5*12？

样本标签：

5*6的矩阵，第一行有6列，每一列代表一个分类，那么就是选1、2、3、4、5或者不选（也就是不满足）。

图形表示：

神经网络

训练五个同样结构的神经网络，每一个指示其中一类VNF的选取。

def my_net(input_len = (5,5,12), classes = 6 ):
    
    X_input = Input(input_len)
    
    # padding to 6 * 6
    X = ZeroPadding2D((1, 1))(X_input)
    
    # first conv
    X = Conv2D(filters = 64, kernel_size = (3, 3), strides = (1,1), padding = 'same', name = 'conv1', kernel_initializer = glorot_uniform())(X)
    X = BatchNormalization(axis = 3, name = 'bn1')(X)
    X = Activation('relu')(X)
    
    # second conv
    X = Conv2D(filters = 128, kernel_size = (3, 3), strides = (1,1), padding = 'same', name = 'conv2', kernel_initializer = glorot_uniform())(X)
    X = BatchNormalization(axis = 3, name = 'bn2')(X)
    X = Activation('relu')(X)
    
    # Pooling
    X = MaxPooling2D((2, 2), strides=(2, 2))(X)
    
    # output layer
    X = Flatten()(X)
    X = Dense(512, activation='relu', name='fc1', kernel_initializer = glorot_uniform())(X)
    X = Dropout(0.5)(X)
    X = Dense(classes, activation='softmax', name='fc2', kernel_initializer = glorot_uniform())(X)

    model = Model(inputs = X_input, outputs = X, name='SFC_Net')
    
    return model

训练集样本：

$ print(X_train.shape, Y_train.shape)

(100000, 5, 5, 12) (100000, 5, 6)

测试集样本：

$ print(X_test.shape, Y_test.shape)

(10000, 5, 5, 12) (10000, 5, 6)

样本中大约10%的样本为当前不能服务。

训练次数：

epoch = 100。

测试集上精度：

单神经网络精度（单类VNF选择）：88.58 %

总精度：58.12%