Description:
Given a string S and a string T, find the minimum window in S which will contain all the characters in T in complexity O(n).
For example,
S = “ADOBECODEBANC”
T = “ABC”
Minimum window is “BANC”.
Note:
If there is no such window in S that covers all characters in T, return the empty string “”.
If there are multiple such windows, you are guaranteed that there will always be only one unique minimum window in S.
题目理解:
给定一个字符集合T,要找到字符串S中包含这些字符的最小子串,字符可以重复,要求复杂度为O(n)。
想了很久也不知道如何O(n),只能想到O(mn)。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| class Solution {
private class CharInt {
char c;
int idx;
CharInt next = null;
public CharInt ( char c, int idx ) {
this.c = c;
this.idx = idx;
}
}
public String minWindow(String s, String t) {
char[] ss = s.toCharArray(), tt = t.toCharArray();
CharInt head = new CharInt('0', -1), tail, relay, temp;
relay = new CharInt(tt[0], -1);
head.next = relay;
for ( int i = 1; i < tt.length; i++ ) {
relay.next = new CharInt(tt[i], -1);
relay = relay.next;
}
tail = relay;
int min = Integer.MAX_VALUE, l = -1;
for ( int i = 0; i < ss.length; i++ ) {
relay = head;
while ( relay.next != null ) {
if ( relay.next.c == ss[i] ) {
temp = relay.next;
temp.idx = i;
if ( temp != tail ) {
relay.next = temp.next;
temp.next = null;
tail.next = temp;
tail = temp;
}
int ll = head.next.idx;
if ( ll != -1 ) {
int len = i - ll + 1;
if ( len < min ) {
min = len;
l = ll;
}
}
break;
}
relay = relay.next;
}
}
if ( l == -1 )
return "";
return new String(ss, l, min);
}
}
|
复杂度:O(mn)。
运行时间:165ms。
击败:3.94%
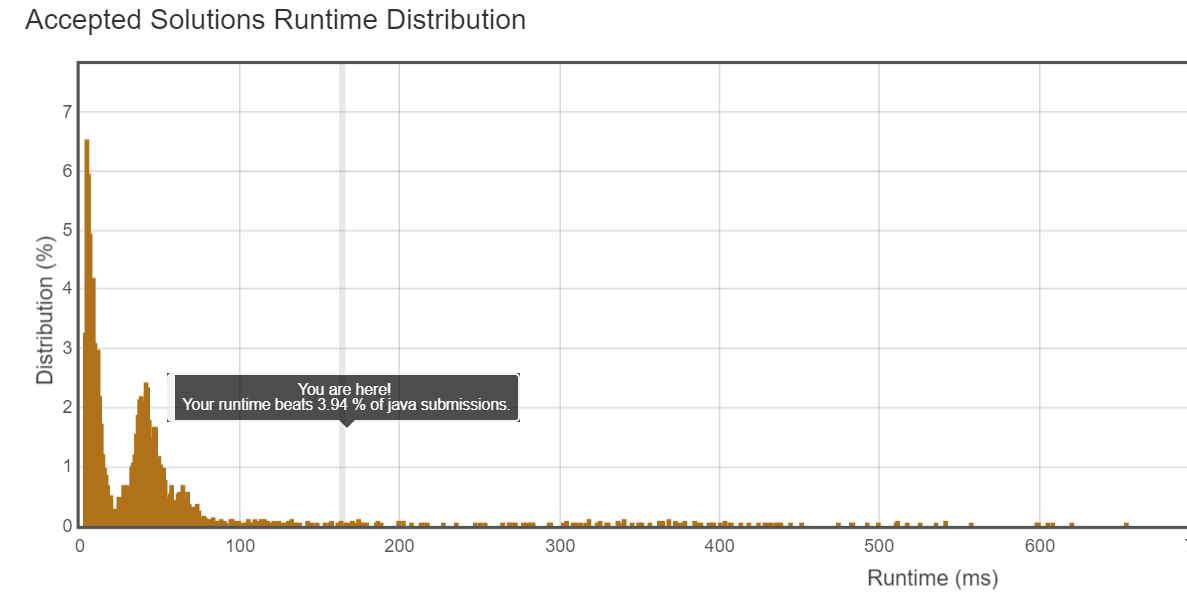
显然复杂度太高,别人都在10ms内,这代码辣鸡。
代码2:
看了别人的代码,总于明白他们是如何做到O(n)。
首先,这里的字符其实只有Ascii码里面的前128个字符,其次java里面的char是可以之间当成int来使用的,
那么这里在匹配字符的时候,就可以直接使用散列表的思想,申请一个128长的int数组就好了。
另外,即使能在O(1)的时间将一个字符匹配到它该在的位置上,那么怎么去找这么一个最小窗口又是一个大问题。
这里的思路实在是巧,首先统计字符集合之后,int[128]上就记录了每一个字符的个数。要想在O(n)的时间内完成,
那么肯定又要用到滑动窗的思路来统计。那么定义这个窗口,窗口的左边界到右边界内的字符能够满足字符集合,并且左边界一定不能再向右移动。
同30题很像,但是这里更加巧妙,只需要在这么个int[128]的数组上进行操作就行:
- 定义距离dis,窗口里面每少一个字符,距离加一,初始化距离为字符集合的总大小。
- 右边界右移,输入一个字符,int[128]上对应位置值减1,然后判断:
- 如果这个位置的值大于等于0,说明这个位置是集合中有的字符,并且现在窗中个数还不足,所以dis减1。
- 如果这个位置的值小于0,那么这个位置:
- 本来就不是集合中的字符,不操作。
- 是集合中的字符,但是窗中这个字符太多,以至于为负,同样不需要操作。
- 当前距离dis为0,说明窗中包含了集合中所有字符,但是可能有多的,于是尝试移动左边界,并保持dis为0:
- 设左边界对应字符A:
- 如果此时A在int[128]上对应位置值等于0,说明此字符是集合需要的字符(否则这个位置的值该为负),并且现在的个数刚刚好,那么左边界不移动。
- 否则int[128]上对应位置值减1。
- dis等于0,尝试更新最小窗口。
通过上面的方法,代码变得非常简单,并且复杂度O(n),额外操作也非常少,甚至空间开销都是固定的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public String minWindow(String s, String t) {
int[] counts = new int[128];
for ( int i = 0, bound = t.length(); i < bound; i++ )
counts[t.charAt(i)]++;
int dis = t.length(), min = Integer.MAX_VALUE, l = -1;
for ( int i = 0, ll = 0, bound = s.length(); i < bound; i++ ) {
counts[s.charAt(i)]--;
if ( counts[s.charAt(i)] >= 0 )
dis--;
while ( dis == 0 && counts[s.charAt(ll)] != 0)
counts[s.charAt(ll++)]++;
if ( dis == 0 && (i - ll + 1) < min ) {
min = i - ll + 1;
l = ll;
}
}
return l == -1 ? "" : s.substring(l, l + min);
}
}
|
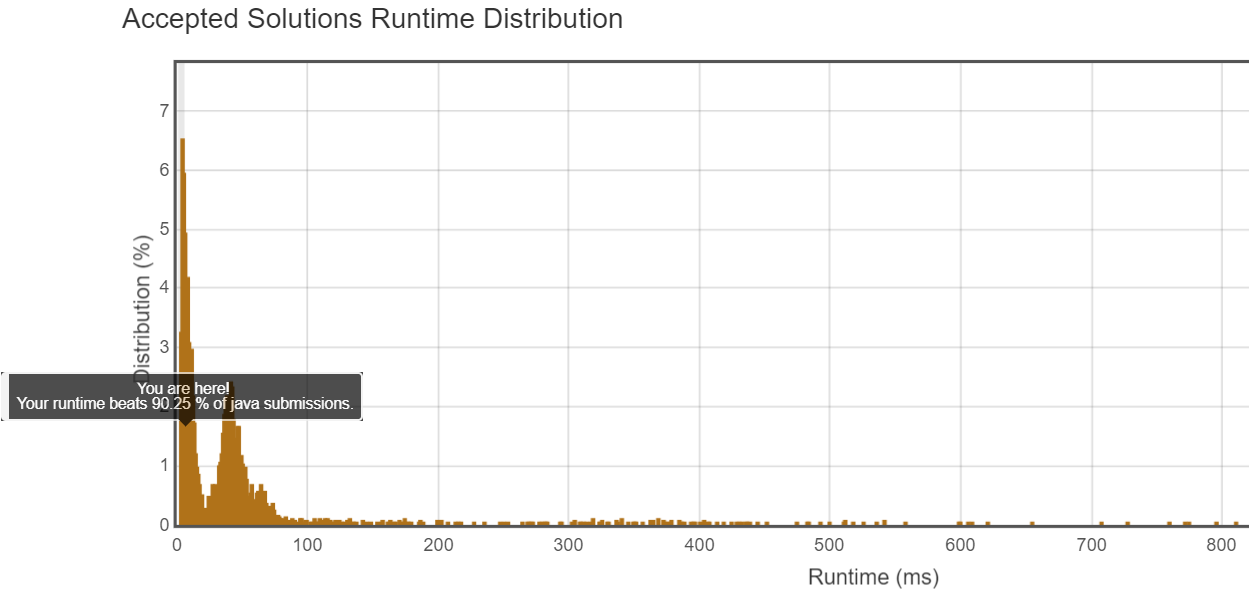
复杂度:O(n)。
运行时间:4ms。
击败:90.25%