龙

哇咔咔

0%

LeetCode 5 Longest Palindromic Substring

发表于 更新于 分类于 Disqus：
Leetcode第5题，最长回文串。

Description:

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example:

Input: “babad”
Output: “bab”
Note: “aba” is also a valid answer.

想法，最简单的，就是以每个字母为中心，向两边扩散，这样的复杂度就是O(n^2)。

那么下面就是第一份代码，就是简单的向两边扩充。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
public class Solution {
    public String longestPalindrome(String s) {
      char[] s_split = s.toCharArray();
        int p, q;
        int index1 = 0;
        int index2 = 0;
        for (int i = 0 ; i < s_split.length ; i++) {
            p = i - 1;
            q = i + 1;
            while ( p >= 0 && q < s_split.length ) {
                if ( s_split[p] == (s_split[q]) ) {
                    p--;
                    q++;
                } else {
                    break;
                }
            }
            if ( ( q - p - 1 ) > ( index2 - index1 + 1 ) ) {
                index1 = p + 1;
                index2 = q - 1;
            }
                    
            if ( i - 1 >= 0 && s_split[i] == s_split[i-1] ) {
                p = i - 2;
                q = i + 1;
                while ( p >= 0 && q < s_split.length ) {
                    if ( s_split[p] == s_split[q] ) {
                        p--;
                        q++;
                    } else {
                        break;
                    }
                }
            }
            if ( ( q - p - 1 ) > ( index2 - index1 + 1 ) ) {
                index1 = p + 1;
                index2 = q - 1;
            }
        }
        return ( new String(s_split, index1, index2 - index1 + 1));
    }
}

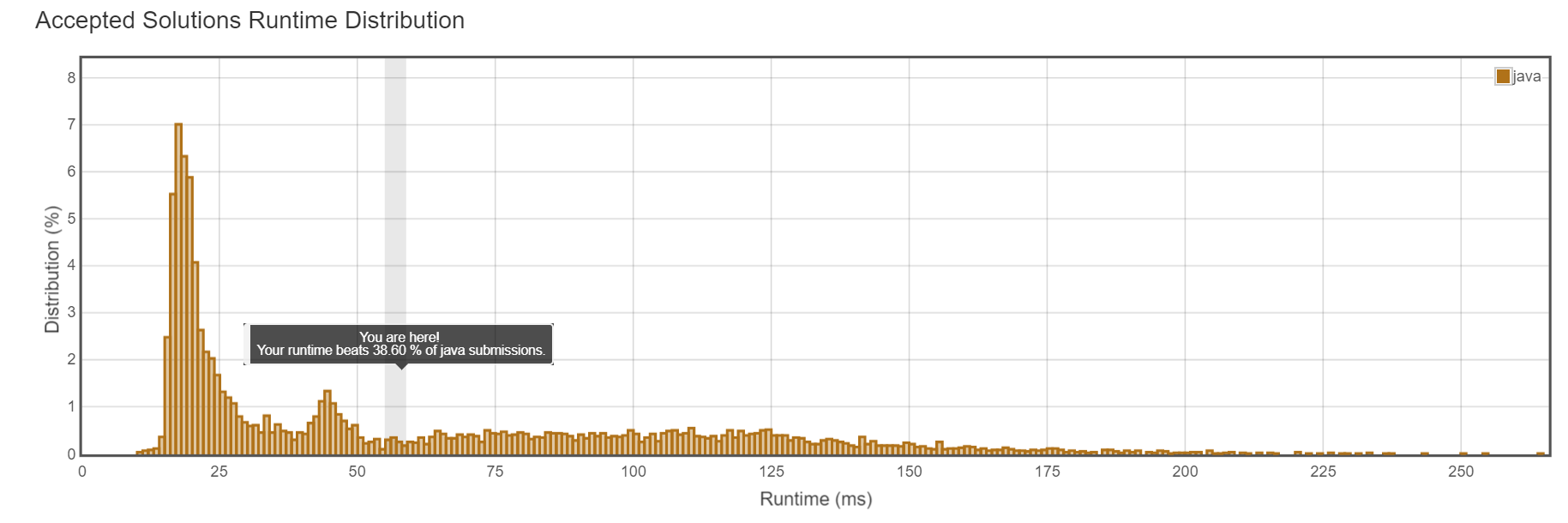
image

击败38.60%，从图上就可以看出来，很垃圾。

时隔不知道多少个月，重新回来发现这么垃圾，索性修改了一下，现在的想法就比较复杂了。

首先，对于一个回文串，它的构成是例如abcdcba的形式，当去掉两边的a时，它依旧是一个回文串bcdcb。

那么如果想要降低复杂度，那么循环到一个字符时，一定要用到之前的信息，这样就能降低复杂度。

通过这种信息论的想法，加上上面回文串的特点，下面是新的算法思路：

  • 循环一遍字符串。
  • 以前一个字符所在的回文串，看以当前字符串为右边界能否去扩张这些字符串。
  • 查看当前字符与前两个字符能否组成回文串，查看能否与前一个字符组成回文串。
  • 保存下当前字符所在的回文串。
  • 当前回文串的长度是否超过之前保存的最长，是则保存。

例如字符串sabckcbaga，假如现在循环到了后一个b，也就是现在前面的字符串是sabckcb，那么前一个字符就是c， 它所在的一个回文串就是ckc，那么现在就尝试用b去扩充它，发现bckcb，可以扩充，所以最长支付串保存为bckcb， 当前所在回文串保存bckcb。再查看kcb是否回文串，不是，查看cb是否回文串，也不是。 那么当前回文串就是bckcb。

循环到下一个字符是a，尝试用a扩充bckcb，扩充成功，当前字符串保存abckcba，最长长度更新， 查看cba不是回文串，查看ba不是回文串。当前回文串abckcba。

再循环到g，尝试扩充abckcba失败，bag、ag也不是回文串，当前回文串没有。

循环到a，上一个回文串没有，查看aga是回文串，ga不是回文串。当前回文串aga。

再例如字符串abababa。

循环到第二个b，它不能扩充前一个回文串aba，bab是回文串，ab不是。当前回文串bab。

循环到a，它能扩充bab，为ababa，同时aba也是回文串，ba不是。当前回文串ababa、aba。

循环到b，它不能扩充ababa，它能扩充aba为babab，同时bab是回文串，ab不是。当前回文串babab、bab。

…

代码里面还考虑了重复，例如aaaaaa，按照上面的操作到第5个a时，它的当前回文串会有aaaaa、aaaa、aaa、aa，这样很不好， 实时上，这里只需要aaaaa，在存一个是否连续的标志位。

例如循环到最后一个a，它上一个回文串为aaaaa，同时连续标志位为true，首先它不能扩充aaaaa，当连续标志位为true时， 看它能否右扩充aaaaa，也就是aaaaa + a是否为为回文串，这里显然aaaaaa是回文串。同时由于连续标志位为true，这里不再需要查看aaa和aa是否为回文串。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
public class Solution {
    
    private int begin = 0;

    private int max_len = 1;
    
    private int p_idx = 0;
    
    private int t_idx = 0;
    
    private void addLen( int[] a, int i, int len ) {
        if ( max_len < len ) {
            max_len = len;
            begin = i;
        }
        if ( i - 1 >= 0 )
            a[t_idx++] = i - 1;
    }
    
    public String longestPalindrome(String s) {
        if ( s == null || s.length() == 0 ) return "";
        char[] ss = s.toCharArray();
        int succ_idx = -1;
        int[] p = new int[ss.length];
        for ( int i = 1; i < ss.length; i++ ) {
            for ( int j = 0; j < p_idx ; j++ )
                if ( ss[p[j]] == ss[i] ) 
                    addLen(p, p[j], i - p[j] + 1);
            if ( succ_idx != -1 ) {
                if ( ss[succ_idx] == ss[i] )
                    addLen(p, succ_idx, i - succ_idx + 1 );
                else succ_idx = -1;
            } else {
                if ( i - 2 >= 0 && ss[i - 2] == ss[i] )
                    addLen(p, i - 2, 3);
                if ( i - 1 >= 0 && ss[i - 1] == ss[i] ) {
                    succ_idx = i - 1;
                    addLen(p, i - 1, 2);
                }
            }
            p_idx = t_idx;
            t_idx = 0;
        }
        return ( new String(ss, begin, max_len));
    } 
}

期望复杂度O(n)？反正最差复杂度O(n^2)。

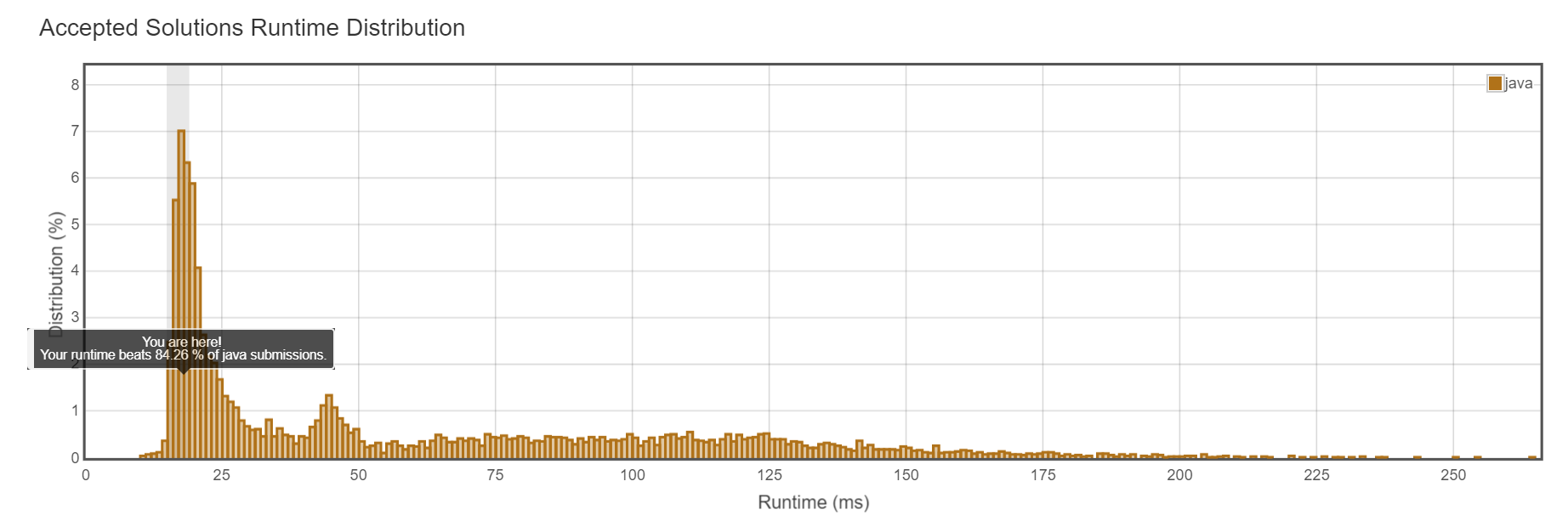
image

击败84.26%，我觉得还行。我甚至觉得如果用例再多一些，可以击败更多的人！！！