Hyperparameter tuning
调参是训练神经网络中十分重要的一项技能,很有可能为了训练出一个好的模型,一大半的时间需要花费在调参上面。
首先调参时要分清楚哪些是重要参数,也就是对结果影响较大的参数,着重去调整它们,例如下列的参数:
- $\alpha$
- $\lambda$
- $\beta_1,\beta_2,\epsilon$
- $layers$
- $hidden \ units$
- $learning \ rate \ decay$
- $mini \ batch \ size$
显然,其中比较重要的参数是$\alpha,\lambda,layers,learning \ rate \ decay$,所以在调参的时候着重去调整它们, 剩下的参数随意一点,可调可不调,看着具体的问题来选择。
通常会认为调参是下面这种形式:
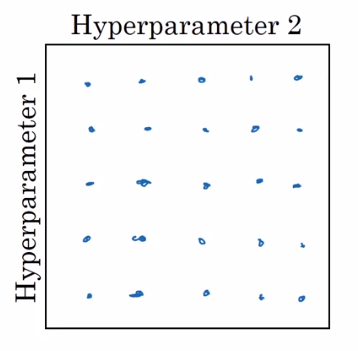
这种形式就是先选好固定的距离,然后进行搜索,这样并没有太大问题,但就上图来说,如果参数一重要,参数二不重要, 这样就会浪费一些搜索机会,比如先固定了参数一,参数二变化五次,这五次模型的性能并不会有什么变化。
所以,可以进行随机选点:
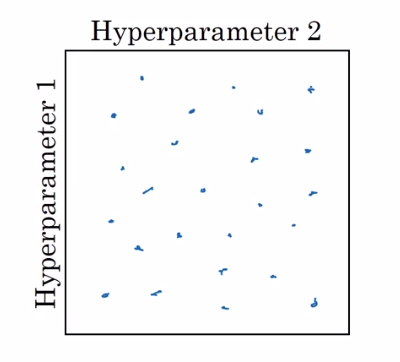
这样就不会太浪费选点的机会。
另外可以第一轮先在一个较大的范围去选点,然后再缩小到一个小一点的范围进行更加精确的搜索。
随机选点:
随机选点可不是random就可以了,有时还需要考虑一下尺度问题,
首先,假如是一个50 ~ 100范围内的随机,那么随机选就可以了,没什么问题,
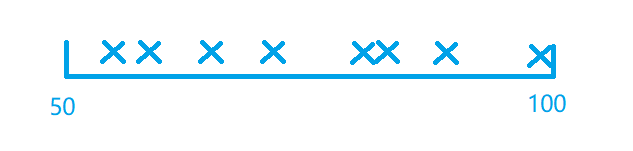
但是如果是一个0.0001 ~ 1的范围,那么随机就会显得很蠢,
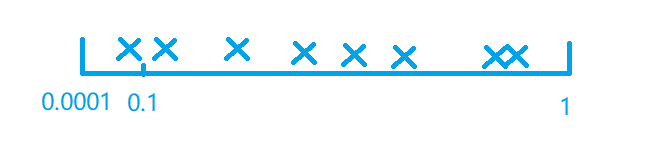
那么90%的概率点会选在0.1 ~ 1的区间里面,显然不行。如下图所示,才是这里的”均匀”。
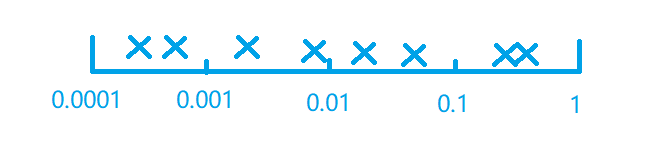
为了产生这种效果,就把它变成一个对数坐标,在python中就像下面这样来写就行了,
1 | r = -4 * np.random.rand() # -4 ~ 0 |
相当于变成对数坐标,在对数坐标上面进行随机,然后再返回来。
如果是一个0.9 ~ 0.999的范围,先按上面的方式随机一个0.1 ~ 0.001的范围,再用1来减就行了。
另外例如范围0.9000 ~ 0.9005与0.999 ~ 0.9995,看起来它们之间没有什么不同,但是实际上,后一个范围它很接近1,
这个变化在机器学习中是会有质变的,所以第二个范围在进行搜索时,需要更加的细致。
另外视频中还给提供了在模型训练时间很长的时候(几天以上),两种调参方式的有趣的名字:
- Pandas:一次一胎,也就是同时只训练一个模型,然后你看着代价变化曲线,每天调一调参。(计算资源较少)
- Caviar:一次n胎,同时训练n个模型,几天后选择其中那个最好的。(计算资源很多)
Batch Norm
就像前面将输入进行标准化一样,可以在神经网络中任意一层去应用类似的标准化方法,这样的标准化对于梯度爆炸和梯度消失问题的缓解都很有好处。
如下图,
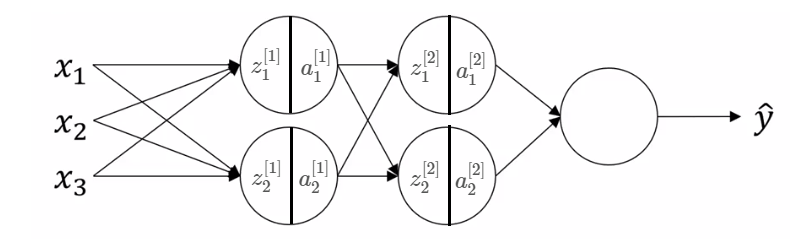
Batch norm一般是在$z^{[i]}$上进行,也就是在激活函数之前进行,
这里的$\epsilon$就是防止出现除以零的错误,另外,这里不直接使用标准化后的$z^{[l]}_{norm}$, 而是加入了两个参数$\delta,\beta$,这两个参数不是定死的,它是随着更新而更新的,加这两个参数的原因, 是为了让模型可以在标准化的基础上进行一下小变动,甚至可以返回标准化之前的数值,例如,
那么带进去计算就会发现,数值又返回原始的状态了。
在这里,使用了Batch norm的层就多了两个参数$\delta,\beta$,在反向传播时,同样要去计算这两个参数的梯度,然后更新。
同样的也可以使用Adam方法来更新这两个参数。
另外需要注意的是,
那么在对$z^{[l]}$进行batch norm的时候,$b^{[l]}$就会显得很多余,因为它会被零均值化掉,
所以在施加了batch norm的神经层中,就不再需要$b^{[l]}$这个参数。
为什么Batch norm会起到作用?
吴恩达在这里给了一些直觉来使得它make sense,例如下面训练一个简单的神经元,
训练的数据如下图左边,测试时变为了下图右边,
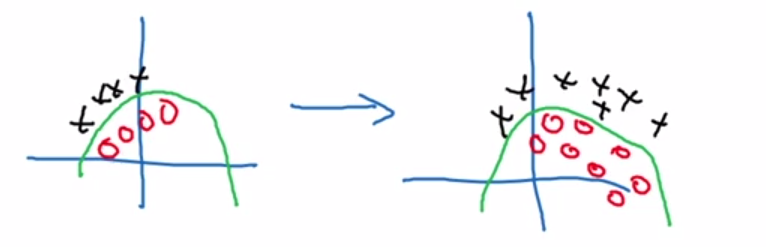
显然由于数据的分布发生了变化,模型的准确率就会下降,不可能指望左边真的能够学习到那条绿色的判决线。
同样的道理,在多层的神经网络中,可以认为某一层的输入就有一个疯狂变化的分布,
那么,这时受到分布变化的影响,这一层就很难去学习到一个比较好的参数。当加上Batch norm时,
就能限制一下这个分布的变化,减轻影响。
测试样本怎么办?
当训练时,使用的都是mini-batch,自然可以计算出它们的均值、方差,但是如果在测试时,一次只有一个样本通过,
那么怎么Batch norm呢?
通常情况下,追踪训练中的每一个mini-batch在该层上得到的均值与方差,使用exponentially weighted的方法来估计它们的均值,
这里的$i$代表第$i$个mini-batch。
注意这样求出来的总的均值、方差只是在test阶段使用,并不用在训练过程中。
梯度怎么求?
这个现在先避开,感觉上就不好算,按吴恩达的说法,通常不会去手写这个的,让学习框架来就好。
Softmax Regression
深度学习框架
不知道视频是什么时间做的,总之上面列出了很多深度学习的框架,但就现在这个时间点来说,TensorFlow肯定是主流的, 当然,课程里面用的也是TensorFlow。
当神经网络的结构变得复杂的时候,手写代码就真的会比较辛苦,还容易出现bug,这个时候,就需要框架来帮忙了。