Mini-batch 和权重更新策略

Mini-batch

在训练时，对样本的输入有三种策略，

一次输入一个样本，Stochastic gradient descent。
一次输入多个样本，Mini-batch gradient descent。
一次输入所有样本，Batch gradient descent。

对于一次输入所有样本，也就是Batch gradient descent，那么每次梯度下降都会向着全局最优/局部最优去前进，这样的缺点就是计算更新很慢，因为一次更新都需要计算整个训练集，在训练集非常大的时候甚至是不可能的。另外，这样更新是很难跳出局部最优的，虽然局部最优也不差，但是总是有差的局部最优。

对于一次输入一个样本，也就是Stochastic gradient descent，那就是向另外一个极端去前进，每次梯度下降都会向着这一个样本的全局最优去前进，虽然这样计算块，更新快，但是随机性也太大了。

对于一次输入多个样本，也就是Mini-batch gradient descent，这就是一个折中的解决方案，每次计算不会太复杂，也能降低一点随机性。

在Mini-batch大小的选择中，一般选取2的幂次的大小，这与CPU/GPU的计算位数相关，所以一般情况，选取64、128、256、512。

权重更新

在梯度下降的基础上，对更新策略更新一下改动，不再是单纯的减去梯度，而是用带有平均的一种思想去更新。

Exponentially weighted averages:

如下图是一个气温随日期变换的坐标图，其中蓝色的点就是某一天的气温，这里总共有一年的数据，

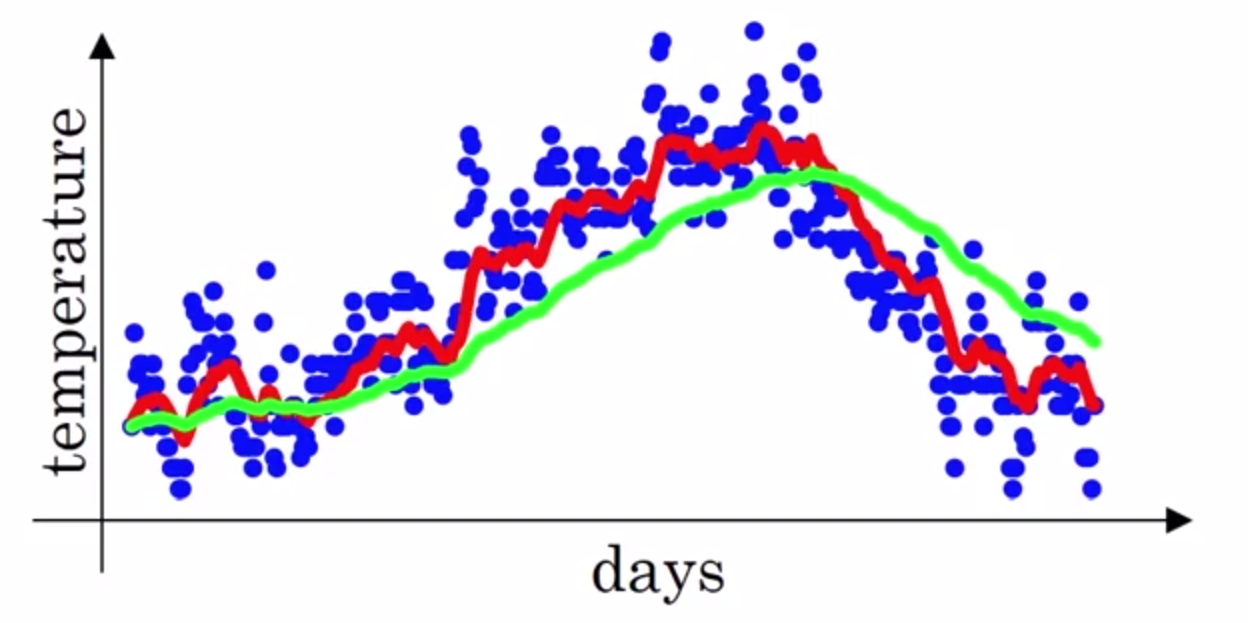
其中红色和绿色的线是根据下面的公式画出来的，

$v_t = \beta v_{t-1} + (1 - \beta)\theta_t$

其中$\theta_t$表示的就是第$t$天的气温，当$\beta = 0.9$时，画出的就是红色的线，当$\beta = 0.98$时，画出的就是绿色的线。上面的式子就相当于是在给气温做平均。

大概平均的天数为：

$days \approx \frac{1}{1 - \beta}$

于是红色的线大概是10天的平均，绿色的线大概是50天的平均，所以绿色的线看起来会有一点偏右。

计算时，就一步一步运算就行了，

$v_\theta = 0$ $v_\theta := \beta v + (1 - \beta)\theta_1$ $v_\theta := \beta v + (1 - \beta)\theta_2$ $...$

但是，在实际操作中，按照上面的式子得到的绿色的线其实应该在紫色的线的位置上，这是因为初始值为0的原因，

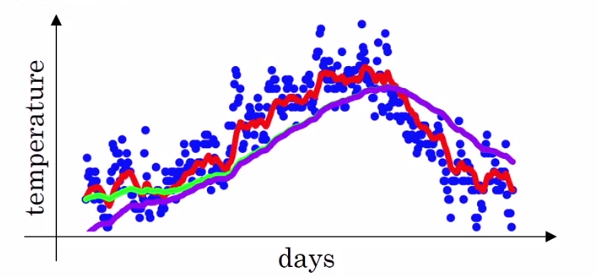
所以，这里需要加入Bias correction，

$v_t = \frac{v_t}{1 - \beta^t}$

这里的$\beta^t$是$\beta$的$t$次幂，刚开始的时候分子会很小，然后逐渐变大，事实上，第一轮迭代，$v_1$就等于$\theta_1$。这样，就能矫正这个初始值太低的问题。

Momentum:

属于权重更新的初级魔法：

$V_{dw} = \beta V_{dw} + (1 - \beta)dw$ $V_{db} = \beta V_{db} + (1 - \beta)db$ $w := w - \alpha V_{dw}$ $b := b - \alpha V_{db}$

通常取$\beta = 0.9$，而且这里不需要矫正。也可以去掉$(1 - \beta)$，变为，

$V_{dw} = \beta V_{dw} + dw$ $V_{db} = \beta V_{db} + db$

这样相当于参数调整基本交给$\alpha$来做。

RMSprop:

属于权重更新的中级魔法：

$S_{dw} = \beta S_{dw} + (1 - \beta)dw^2$ $S_{db} = \beta S_{db} + (1 - \beta)db^2$ $w := w - \alpha \frac{dw}{\sqrt{S_{dw}}}$ $b := b - \alpha \frac{db}{\sqrt{S_{db}}}$

这里的$dw^2$就是$dw$的平方，当然也是element-wise的。这里的$\beta$通常取0.999，而且也不用矫正。

为了防止出现分母为0的错误，通常要在分母上加上一个很小的数$\epsilon$，

$w := w - \alpha \frac{dw}{\sqrt{S_{dw}} + \epsilon}$ $b := b - \alpha \frac{db}{\sqrt{S_{db}} + \epsilon}$

Adam:

属于权重更新的高级魔法，它将Momentum与RMSprop相结合：

$Init:V_{dw} = 0, S_{dw} = 0, V_{db} = 0, S_{db} = 0$ $V_{dw} = \beta_1 V_{dw} + (1 - \beta_1) dw$ $V_{db} = \beta_1 V_{db} + (1 - \beta_1) db$ $S_{dw} = \beta_2 S_{dw} + (1 - \beta_2) dw^2$ $S_{db} = \beta_2 S_{db} + (1 - \beta_2) db^2$

显然这里的$V_{dw}$属于Momentum，

这里的$S_{dw}$属于RMSprop，

另外这里还要用到矫正：

$V_{dw}^{corrected} = \frac{V_{dw}}{(1 - \beta_1^t)}$ $V_{db}^{corrected} = \frac{V_{db}}{(1 - \beta_1^t)}$ $S_{dw}^{corrected} = \frac{S_{dw}}{(1 - \beta_2^t)}$ $S_{db}^{corrected} = \frac{S_{db}}{(1 - \beta_2^t)}$

将它们结合起来，权重的更新策略就如下：

$w := w - \alpha \frac{V_{dw}^{corrected}}{\sqrt{S_{dw}^{corrected}} + \epsilon}$ $b := b - \alpha \frac{V_{db}^{corrected}}{\sqrt{S_{db}^{corrected}} + \epsilon}$

通常将参数设置为$\beta_1 = 0.9,\beta_2 = 0.999,\epsilon = 10^{-8}$，一般情况不需要去调整它们的取值，默认的就足够了。

（它名字的全称其实是Adaptive moment estimation，所以其实和Adam没有半毛钱关系…）

Learning rate decay

在权值更新的过程中逐渐减小学习速率，能够使模型收敛到更好的解，

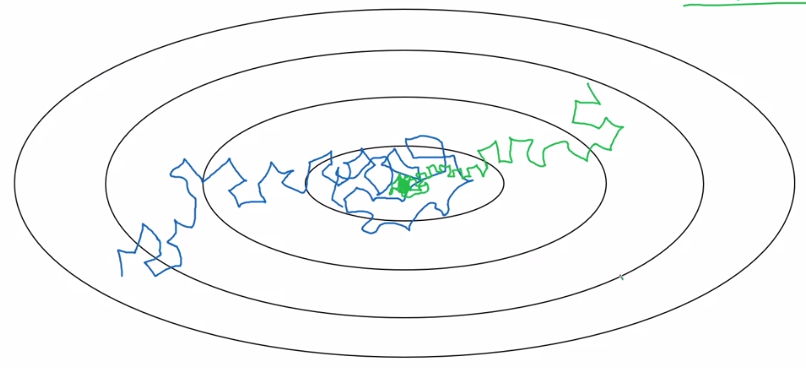
其中蓝色的线是没有减小学习速率的，它最后会在最优解附近一个较宽的范围徘徊，另外绿色的线就是逐渐减小学习速率的，它会收敛到一个较窄的范围。

需要注意的是，这里逐渐减小学习速率的单位是epoch，一个epoch就是过一遍数据。

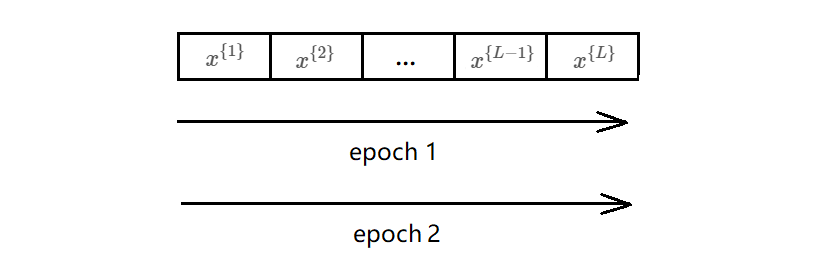
首选的策略是：

$\alpha = \frac{1}{1 + decayRate * epochNum} \alpha_0$

其它的一些策略：

$\alpha = 0.95^{epochNum} \alpha_0$ $\alpha = \frac{k}{\sqrt{epochNum}} \alpha_0$

或者，

$\alpha = \frac{k}{\sqrt{t}} \alpha_0$

这里的$t$就是总的迭代次数了，上面的$k$是一个固定的常量。

以上的这些decay的方法其实都可以，选一个用就好。

关于局部最优

通常对于局部最优的印象是这样的，

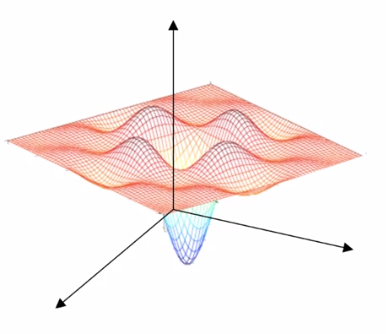
就会觉得很容易陷入局部最优，但是实际上在高维空间中，这样的直觉是不准确的，它更像是下面的马鞍面，

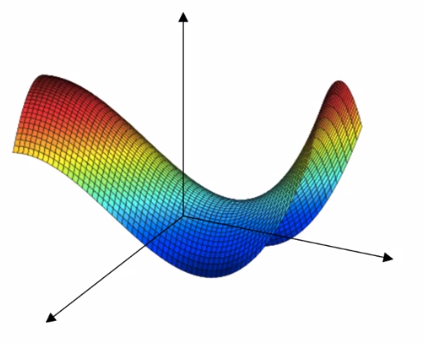
那么在遇到一个梯度为0的点的时候，实际上更可能是马鞍面中间的那个点，模型因为各种措施，它也并不会卡在这个点上。

因为这样的原因，神经网络几乎不可能卡在一个很差的局部最优点上，通常都能收敛到一个较好的局部最优点，距离全局最优也差不了多远。