神经网络的数据集划分、正则化、Dropout、输入标准化以及梯度检查等等

数据集的拆分

在一个数据集上去应用机器学习算法时，你可能可以选择不同的算法，同样的，相同的算法也可以有不同的参数，例如神经网络中的网络层数，神经元个数等等。这个时候当然就得一个一个算法去试，一个一个参数去调，来选出所认为的表现最好的模型。这时就会一个问题，如何去评判哪一个模型在这里最好？

通常情况（默认这里是监督学习），首先需要拿一部分数据出来训练模型，然后在训练完毕后，让训练好的模型去预测另一部分数据，用这部分数据来评判这个模型的性能，这样就能选出最合适的模型。

但是这里得到模型准确率是不能作为模型的真实准确率的，因为这里相当于用同一份数据去在一堆模型中选出最好的模型，这样就可能是因为这个模型刚好符合这部分数据而已，所以需要用“新”的数据来测试这个模型的准确率。

综上，数据的划分为训练集 + 交叉验证集 + 测试集，视频中的原英文是Training Set + Development Set/Hold-out Cross Validation Set + Test Set。

这三部分的划分比例一般为70% + 20% + 10%，但是这个比例并不是一定的，只要能实现各个部分的功能就行，例如有一百万的样本，也许一万个样本对于交叉验证集来说已经足够了。

正则化

正则化可以说是神经网络必不可少的一个部分，因为神经网络的拟合能力十分强大，所以它的过拟合能力也是十分的强大。事实上，神经网络中很多的技巧都是为了去减少过拟合，正则化是其中最基础的一个。

$J(w^{[1]},b^{[1]},...,w^{[L]},b^{[L]}) = \frac{1}{m} \sum_{i=1}^m L(\hat y^{(i)}, y^{(i)}) + \frac{\lambda}{2m} \sum_{l = 1}^L ||w^{[l]}||_F^2$

上面的公式就是加了正则化的代价函数，也就是多了一项权重的2-范数，这样就会将权重的取值大小考虑到代价函数里面。

由于优化目标是最小化代价函数，那么正则化项的存在就会迫使权重的取值变小，权重的取值不再那么自由，它就会选择一个折中，不再过分的变化某些权重来迎合训练数据，达到减轻过拟合的目的。

另外这里多了一个参数$\lambda$，这个参数就控制着正则化的强度，也就多了一个训练时需要调整的超参数。

加上正则化项对于反向传播的求导也没有什么影响，在之间的基础上加上正则化项的导数就行，

$dw^{[l]} = (from \ backprop) + \frac{\lambda}{m}w^{[l]}$

对于偏置项$b^{[l]}$来说，可以对它正则化，也可以不正则化，不重要。这里具体的原因还不知道，感觉它取值其实是受到权重影响的，在对权重加上偏置之后，它加不加偏置就变得不重要了。

注：正则化又叫weight decay。

Drop Out

Drop-out是一个很神奇的东西，它同样可以减小神经网络过拟合，提高模型的泛化能力。

它的操作就是给予每个神经元一定的几率使它会被“丢弃”掉，如下图，

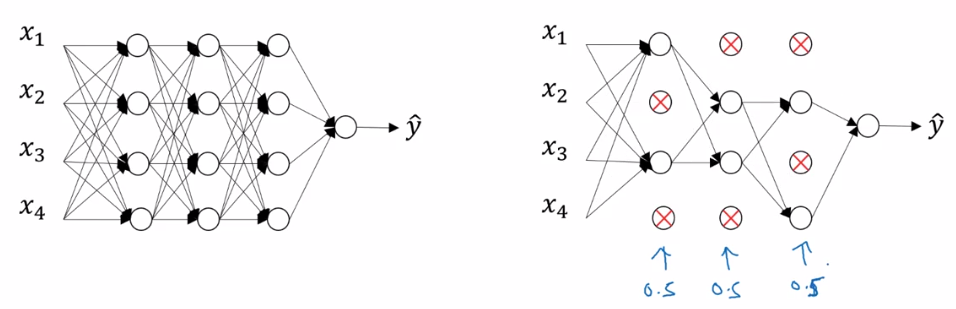
图中以50%的几率使得一些隐藏层的神经元抑制，也就是不往后传播。

直观意义上来说，由于每次都会有不同的神经元被抑制，所以模型不能只依靠某些神经元，这里如果第一层也使用Drop-out，那么就意味着输入的一些属性也会被抑制掉，这就迫使每一个神经元都得有作用，或者不能依赖样本的某一个属性，而且它们的功能上也要有冗余。于是模型就不会过分的去拟合当前数据，也就达到了减小过拟合的目的。（输出层当然不能加Drop-out）

注意：

加入Drop-out后的梯度运算就和ReLU函数类似，被抑制的神经元就不再反向传播，所以抑制矩阵也需要在前向传播中缓存下来，因为在反向传播时将会用到它。

另外使得每一层的期望输出不会变小，对于没有被“drop-out”的神经元的输出，将它除以drop-out的概率，例如作业中的代码，

D1 = np.random.rand(A1.shape[0], A1.shape[1])  # drop-out矩阵
D1 = ( D1 < keep_prob )                        # 变为0，1
A1 = A1 * D1                                   # drop-out
A1 = A1 / keep_prob                            # 除以概率

因为这里乘上了系数$\frac{1}{keep-prob}$，那么在反向传播求导时，这个系数同样的存在，

1 2	dA1 = dA1 * D1 dA1 = dA1 / keep_prob

另外，在对测试样本进行分类时，关闭Drop-out，也不再乘系数$\frac{1}{keep-prob}$。

其它的一些防止过拟合的方式

Data Augmentation:

不知道如何翻译，总之思想很简单，就是将现有的数据集中的样本进行一下处理，得到一些变化后的样本，将这些变化后的样本也加入训练集，这样也能够提升模型的泛化性能，减轻过拟合。

如下图的图片分类问题，

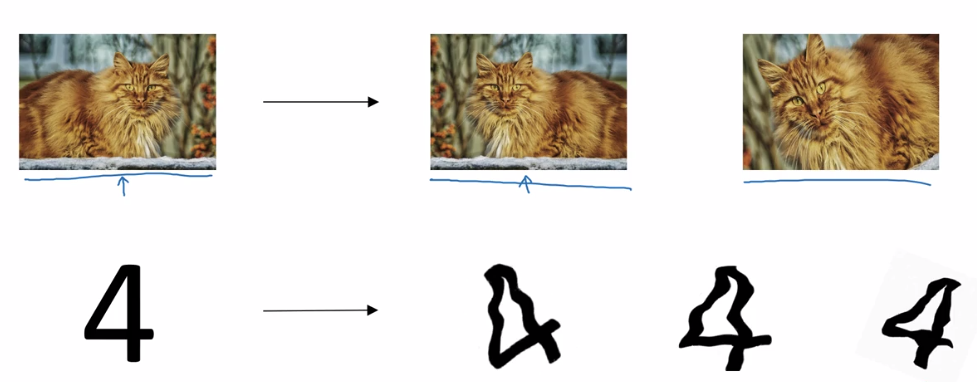
其中左边是原始的图片，将图片安装当前分类的性质，可以进行对称，旋转，噪声等操作，这样就能在原样本上得到新的一些样本，并且这些样本也是在实际中真实会遇到的一些情况。

Early Stopping

直接看图，

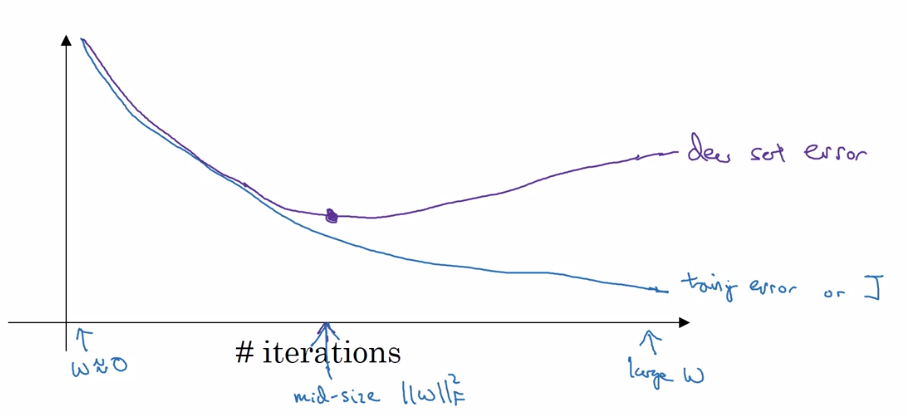
图中的蓝色线就是训练集在模型中的误差，它随着训练逐渐减小。紫色线是dev set在模型中的误差，它随着模型的训练也是逐渐减小，但是当迭代到一定次数的时候，模型就开始过拟合了，于是它的误差就会逐渐增高。

所以Early Stopping的意思就是去提前结束训练，争取不让模型过拟合，所以在训练过程中可以去画这个曲线，提早停止训练。

输入标准化

Normalizing Input，输入标准化是在数据预处理中非常重要的一步，由于原始数据每个属性的取值范围不一样，如果不做处理的话，可能在进行梯度下降时会遇到一些困难，例如，

$x_1 \in \{1-100\}$ $x_2 \in \{1-10000\}$

这时，两个属性之间的差距就会变得很大，如下图，

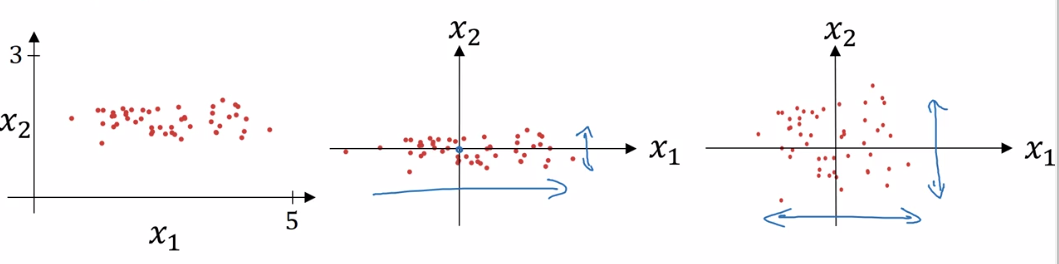
它的样本分布就与左边的图类似，比较狭长。

中间的图是零均值化后的分布。

最右边的图是再进行方差归一化的分布。

公式如下：

$\mu = \frac{1}{m} \sum_{i = 1}^m x^{(i)}$ $\sigma ^2 = \frac{1}{m} \sum_{i = 1}^m (x^{(i)})^2$ $x := x - \mu$ $x /= \sigma ^2$

这里的$x^{(i)}$就是一个样本，它是一个向量，但是这里的操作都是element-wise的。 需要注意的是，这里是先进行零均值化，然后再对零均值化后的样本进行方差归一化，所以方差里面省去了均值0。

下面是输入标准化之前和之后的代价函数的取值空间对比：

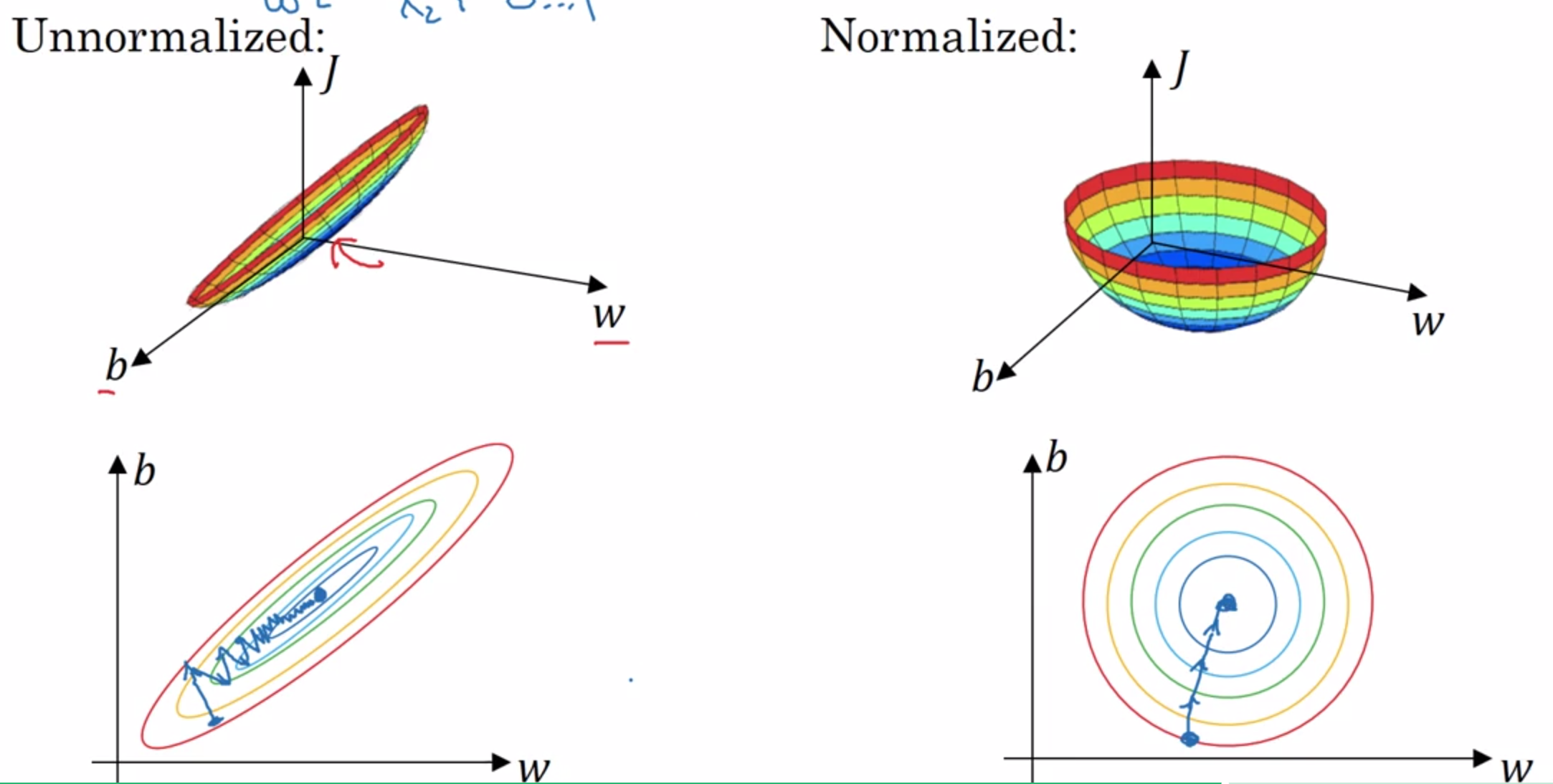
显然在输入标准化之后，能更好的进行优化。

注意：

直接对整个训练集进行标准化，所以能够得到整个训练集的均值和方差，那么在test阶段，输入的样本同样的按照这个均值和方差去标准化就行。

Vanishing/exploding gradients

梯度消失和梯度爆炸是深度神经网络中会遇到的问题，假设一个深度神经网络，如下图：

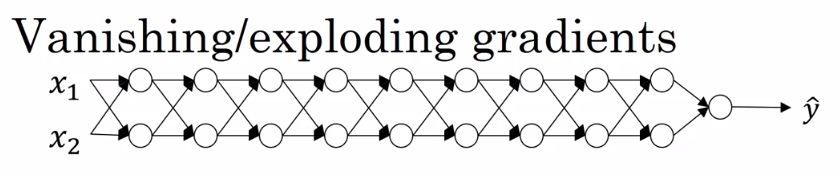
假设这个网络的激活函数是一个线性激活函数，并且没有偏置，

$z^{[l]} = w^{[l]}z{[l-1]}$

那么$\hat y$就可以写为，

$\hat y = w^{[L]}w^{[L-1]}...w^{[2]}w^{[1]}x$

假设中间每一层的神经元权值都相同，

$\hat y = w^{[L]}(w^{[1]})^{(L-1)}x$

那么当$w^{[1]}$取下列值得时候

$w^{[1]} = \begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \end{bmatrix} \ \ \ \ or \ \ \ \ w^{[1]} = \begin{bmatrix} 1.5 & 0 \\ 0 & 1.5 \end{bmatrix}$

在经历$(w^{[1]})^{(L-1)}$之后，显然值要不会非常小，要不就会非常大。这样，要不就是数据太大，直接计算错误，要不就是数据太小，一次迭代和没有迭代一样，这就是问题所在。

（所以和梯度有什么直接关系，为何要叫做梯度消失、梯度爆炸？？？）

权重的初始化

为了减轻上面的梯度爆炸或者梯度消失的问题，在权重初始化时，可以施加一定的规则。

先看一个神经元中$z$的计算，

$z = w_1x_1 + w_2x_2 + ... + w_nx_n$

为了让$z$既不会太大也不会太小，那么让$w$的均值为0，方差为$\frac{1}{n}$，会有一定的帮助。

对于ReLU激活函数，

$w^{[l]} = np.random.randn(shape)*np.sqrt(\frac{2}{n^{[l-1]}})$

这里分子变为了2（为1叫做Xavier Initialization，为2时叫做He Initialization），暂时只知道这是一个经验值。

对于tanh激活函数，分子不用变成2，

$w^{[l]} = np.random.randn(shape)*np.sqrt(\frac{1}{n^{[l-1]}})$

另外这里的也可以选择为，

$\sqrt{\frac{2}{n^{[l-1]}+ n^{[l]}}}$

最后，初始化只是给了一个起始点而已，它并不是一个完美的方法。

梯度检查

在实现神经网络的过程中，可能不注意就写出了一个bug，有时候可能发现不了，那么这时候最好先用梯度检查来看代码是否存在问题，当不存在问题时，再关闭梯度检查。

对于导数，可以利用导数的定义来进行计算，

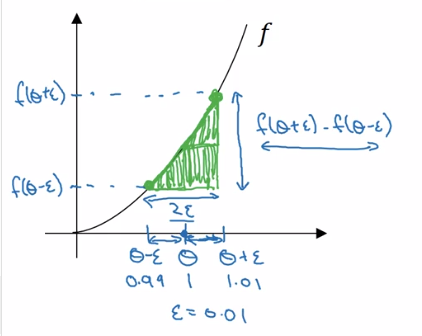
这样，取一个很小的$\epsilon$，就能使用下面公式去近似到$f(\theta)$在点$\theta$的导数。

${f}'(\theta) = \frac{f(\theta + \epsilon) - f(\theta - \epsilon)}{2 \epsilon}$

implementation:

在实现梯度检查时，首先将所有的参数$W^{[1]},b^{[1]},…,W^{[L]},b^{[L]}$合并成一个超长的向量$\theta$，同样的，也将反向传播得到的各个梯度$dW^{[1]},db^{[1]},…,dW^{[L]},db^{[L]}$合并成一个向量$d\theta$。

因为所有参数的导数都是由代价函数$J$求导得来的，那么在求他们梯度的近似的时候，当然要从代价函数入手，

$d\theta_{approxi}^{[i]} = \frac {J(\theta_1,\theta_2,...,\theta_i + \epsilon,...) - J(\theta_1,\theta_2,...,\theta_i - \epsilon,...)} {2\epsilon}$

求出所有参数的近似梯度，将它们与反向传播得到的梯度相比较，

$check \ \ \ \frac{||d\theta_{approxi} - d\theta||_2}{||d\theta_{approxi}||_2 + ||d\theta||_2}$

从经验直觉上，当这个比值在$10^{-7}$往下时，就可以认为这里的梯度计算没有问题；当在$10^{-5}$左右时，就可能会有问题了；当在$10^{-3}$往上时，几乎可以认为一定有问题。

注意事项：

Don’t use in training - only to debug.（梯度检查是一件很费时间的事情，每改一个参数就得计算一次前向传播）
If algorithm fails grad check, look at components to try to identify bug.（定位问题所在）
Remember regularization.
Doesn’t work with dropout.（会变得不好计算，先关闭dropout，检查完毕再开启）
Run at random initialization; perhaps again after some training.