Logistic Regression 简单总结

Logistic Regression

把它看成只有一个神经元的神经网络，激活函数就是sigmoid函数。

模型：

$\hat y = \sigma (W^T x + b)$

其中，

$\sigma(Z) = \frac{1}{1+e^{-Z}}$

代价函数：

$J(W,b) = \frac{1}{m} \sum_{i=1}^m L(\hat y^{(i)},y^{(i)} ) = - \frac{1}{m} \sum_{i=1}^m y^{(i)}log \ \hat y^{(i)} + (1-y^{(i)})log(1 - \hat y^{(i)})$

视频中好像没有具体说这个损失函数的一个推导，这里自己简单推一推。

首先对于$\sigma(Z)$这个函数，它其实就是经常说到的sigmoid函数，它的函数图像如下：

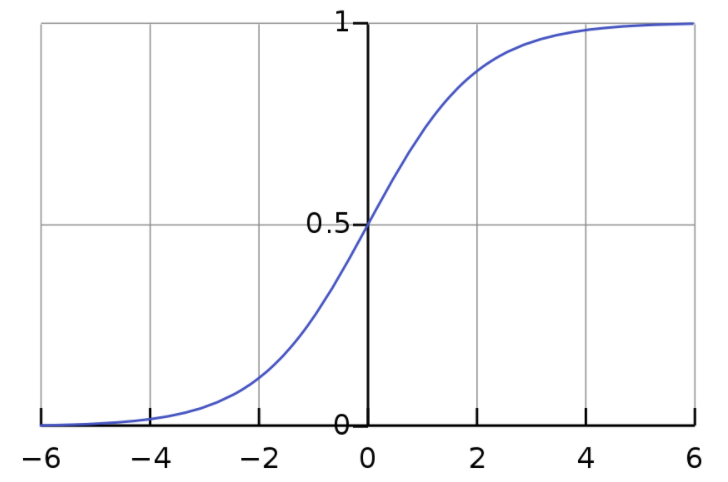
可以看出sigmoid函数的值域范围是0~1，所以通常把它当成一个概率来看待，那么，可以写出y的概率表达式为：

$P(y) = (\hat y)^y (1 - \hat y)^{1-y}$

其中$\hat y$就是预测$y$为1的概率，区分两种情况，上面的式子分开写就是下面的式子，合并在一起有利于公式化：

$P(y) = \begin{cases} \hat y \ \ \ \ \ \ \ \ \ \ ,y = 1 \\ 1 - \hat y \ \ \ ,y = 0 \end{cases}$

所以我们采用极大似然法来进行对$W$的求解，似然函数就可以写为：

$\prod_{i=1}^m (\hat y^{(i)})^{y^{(i)}}(1 - \hat y^{(i)})^{1 - y^{(i)}}$

对数似然写为：

$L(\hat y) = \sum_{i=1}^m y^{(i)}log \ \hat y^{(i)} + (1-y^{(i)})log(1 - \hat y^{(i)})$

加上$- \frac{1}{m}$就得到了上面的代价函数，同时也从最大化变成了最小化。

梯度：

首先需要对代价函数进行求导，下面进行推导，令：

$Z^{(i)} = W^Tx^{(i)} + b \\ \alpha^{(i)}=\sigma (W^Tx^{(i)} + b)$

单独看一个样本 $(x^{(i)},y^{(i)})$ ，它的代价函数为，

$J^{(i)} = y^{(i)}log(\alpha^{(i)})+ (1-y^{(i)})log(1 - \alpha^{(i)})$

对其中一个 $W_i$ 进行求导,这里先忽略上标 $(i)$ ：

$\frac{\partial J}{\partial W_i}= \frac{y}{a} \frac{\partial \alpha}{\partial W_i} - \frac{1-y}{1-\alpha}\frac{\partial \alpha}{\partial W_i} = ( \frac{y}{a} - \frac{1-y}{1-\alpha} )\frac{\partial \alpha}{\partial W_i}$

然后其中的$\frac{\partial \alpha}{\partial W_i}$继续计算：

$\frac{\partial \alpha}{\partial W_i}= \frac{e^{-Z}}{(1+e^{-Z})^2} \frac{\partial Z}{\partial W_i} = \frac {1}{1+e^{-Z}}\frac{e^{-Z} + 1 - 1}{1+e^{-Z}} \frac{\partial Z}{\partial W_i} = \alpha(1 - \alpha)\frac{\partial Z}{\partial W_i}$

继续对$\frac{\partial Z}{\partial W_i}$进行计算：

$\frac{\partial Z}{\partial W_i} = x_i$

将上面的合起来，写为：

$\frac{\partial J}{\partial W_i} = ( \frac{y}{a} - \frac{1-y}{1-\alpha} )\alpha(1 - \alpha)x_i = (y - \alpha)x_i$

注意到代价函数为：

$J(W,b) = - \frac{1}{m} \sum_{i=1}^m y^{(i)}log(\alpha^{(i)}) + (1-y^{(i)})log(1 - \alpha^{(i)})$

所以考虑到向量化处理，同时加上前面的因子$-\frac{1}{m}$，最终可以写为：

$\begin{cases} \frac {\partial J}{\partial W} = \frac{1}{m}X(A - Y)^T \\ \frac {\partial J}{\partial b} = \frac{1}{m} \sum_{i=1}^m(\alpha^{(i)} - y^{(i)}) \end{cases}$

其中，

$A = [\alpha^{(1)},\alpha^{(2)},...,\alpha^{(m-1)},\alpha^{(m)}] \\ X = [x^{(1)},x^{(2)},...,x^{(m-1)},x^{(m)}] \\ Y = [y^{(1)},y^{(2)},...,y^{(m-1)},y^{(m)}]$

参数更新

权值的更新就按照梯度下降的原则更新就行，

$\begin{cases} W = W - \alpha \frac {\partial J}{\partial W} \\ b = b - \alpha \frac {\partial J}{\partial b} \end{cases}$

这里的$\alpha$代表学习因子。

存疑

如果直接使用最小二乘损失函数呢？