DNN 笔记一

关于第一个专项课程的笔记。

这里先简单的定义为DNN就是层数很多的神经网络。

---

激活函数

神经网络的激活函数一般有以下四种：

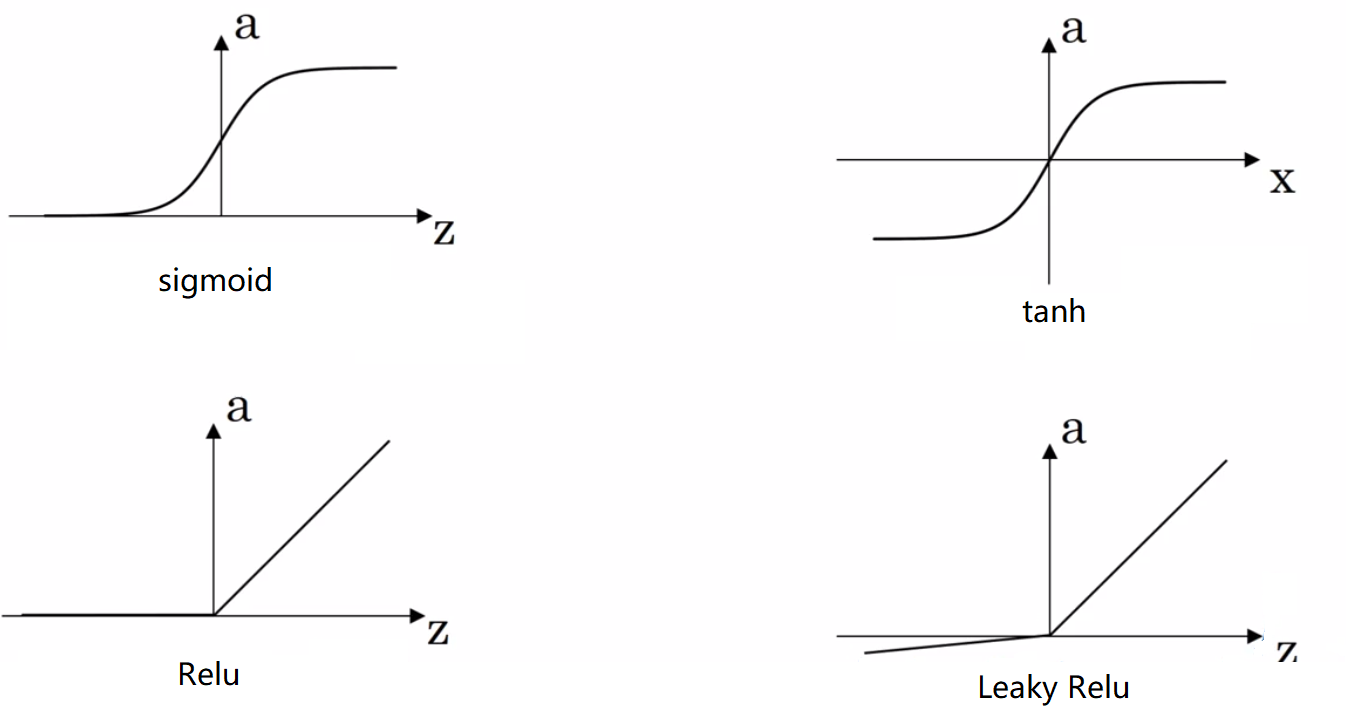
它们的方程写为：

$$sigmoid = \frac{1}{1+e^{-Z}}$$ $$tanh = \frac{e^x-e^{-x}}{e^x+e^{-x}}$$ $$Relu = max(0,Z)$$ $$Leaky Relu = max(0.01Z,Z)$$

从图中可以看出，对于sigmoid函数，它的输出大于1，这对于神经网络来说是不利的。 tanh就能对sigmoid函数进行改进，使得输出值的范围在-1到1之间。

但是，对于sigmoid和tanh来说，当输出值Z过大或者过小时， 当我们在求取梯度的时候，这个地方的梯度值就几乎为0，这样就使得在网络层数较多时， 梯度值在某一层就会变为十分接近0，影响到梯度的反向传播。

所以，一般情况下，使用Relu或Leaky Relu来作为神经网络的激活函数， 它不仅能改善梯度的反向传播，还可以加快训练速度，因为作为函数，它的计算算是非常简单。

对它们进行求导，看它们的导函数长什么样：

对于$g(z) = \frac {1}{1+e^{-z}}$，它的导函数为：

$$\frac{d}{dz}g(z) = g(z)(1 - g(z))$$

对于$g(z) = tanh(z)$，

$$\frac{d}{dz}g(z) = 1 - g(z)^2$$

对于$g(z) = Rule(z) = max(0,z)$,

$$\frac{d}{dz}g(z) = \begin{cases} 0 \ \ \ \ \ ,\mbox{if } z < 0 \\ 1 \ \ \ \ \ ,\mbox{if } z > 0 \end{cases}$$

最后对于$g(z) = LeakyRelu(z) = max(0.01z, z)$ ，

$$\frac{d}{dz}g(z) = \begin{cases} 0.01 \ \ \ ,\mbox{if } z < 0 \\ 1 \ \ \ \ \ \ \ \ ,\mbox{if } z > 0 \end{cases}$$

看得出上面的导数其实都很简单，这也有利于快速的计算。

---

两层神经网络

在week_3的作业中，需要构建一个两层的神经网络，这里将它拿出来先分析一下。

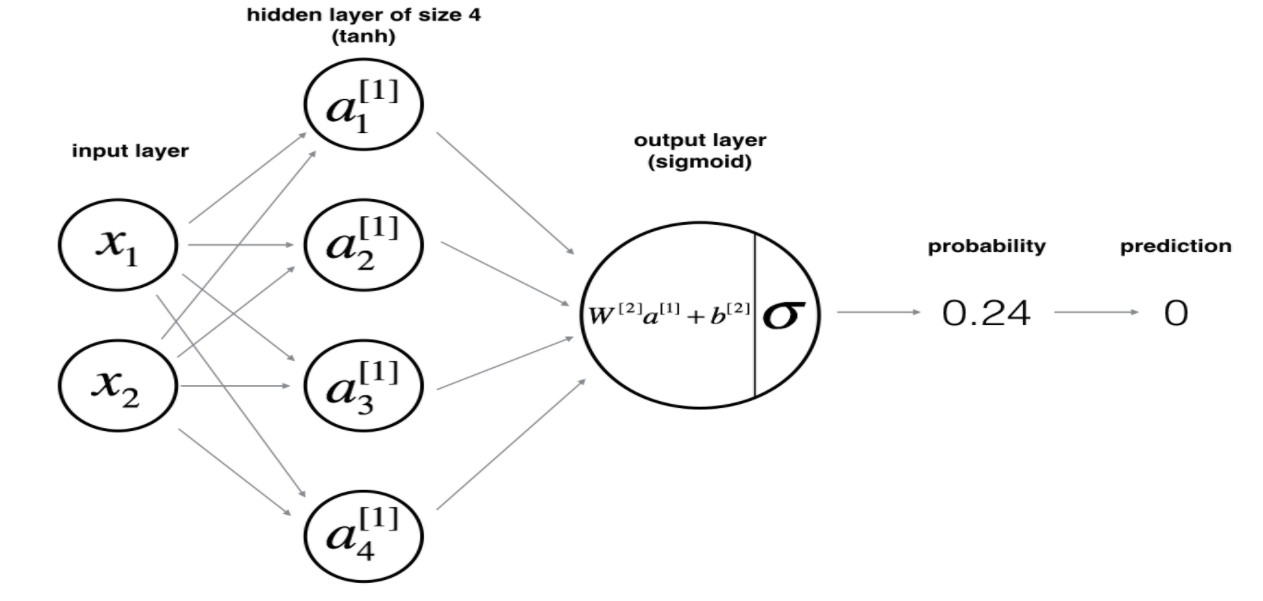
注意到这里的激活函数是tanh加上sigmoid，最后一层使用sigmoid的原因， 主要是为了输出一个0~1的值，就可以把它看成概率来处理。（由图中可以看出其中的上标 $[i]$就代表了层数）

参数初始化

这里需要初始化的参数有：

• 学习速率$\alpha$。
• 链接权值$w^{[i]}$。
• 偏置$b^{[i]}$。

对于学习速率$\alpha$，一般将其定义为一个确定的值即可，可能在0.01~1之间， 视情况而定，需要不断调整来获得它较优的取值。

对于偏置$b^{[i]}$，直接将它初始化为0就可以了。

对于权值$w^{[i]}$，这里就不能将它们初始化0，或者可以说不能将它们初始化为一个相同的值， 因为如果它们的初始值相同，它们之间的更新将不会有差异，这样它们会一直取到相同的值， 显然不行。 （如果使用drop-out策略，初始化为相同的值应该也无所谓）

对于权值的初始化，它的好坏对网络的训练也是会有很大影响的，后面再谈。

这里直接随机初始化就行，

w = np.random.randn(dx,dy) * 0.01

b = np.zeros((dx,1))

这里权值$w$先以标准正态来随机取值，然后乘以0.01，防止权值过大造成计算出的数值过大。 偏置$b$直接初始化为0即可。

前向传播

对于一个输入$x^{(i)}$，它的前向传播过程如下：

$$z^{[1] (i)} = W^{[1]} x^{(i)} + b^{[1] (i)}$$ $$a^{[1] (i)} = \tanh(z^{[1] (i)})$$ $$z^{[2] (i)} = W^{[2]} a^{[1] (i)} + b^{[2] (i)}$$ $$\hat{y}^{(i)} = a^{[2] (i)} = \sigma(z^{ [2] (i)})$$ $$y^{(i)}_{prediction} = \begin{cases} 1 \ \ \ \ \ \mbox{if } a^{[2](i)} > 0.5 \\ 0 \ \ \ \ \ \mbox{otherwise } \end{cases}$$

这里的输出是一个$a^{[2]}$，它是$z^{[2]}$通过sigmoid函数求出来的， 输出的值可以看出一个概率值，所以这里使用一个交叉熵函数来估计最后的损失。

$$J = - \frac{1}{m} \sum_{i=0}^{m} (y^{(i)}log(a^{[2](i)}) + (1 - y^{(i)})log(1 - a^{[2](i)}))$$

反向传播求其梯度：

最重要的，就是函数的反向传播过程了，这也是最难的地方， 但实际上它就是一个求取梯度的过程，但是由于函数嵌套太多， 所以容易引起困扰。

这里先忽略前面的系数，就当输入只有一个样本，所以去掉所有的上标$(i)$。

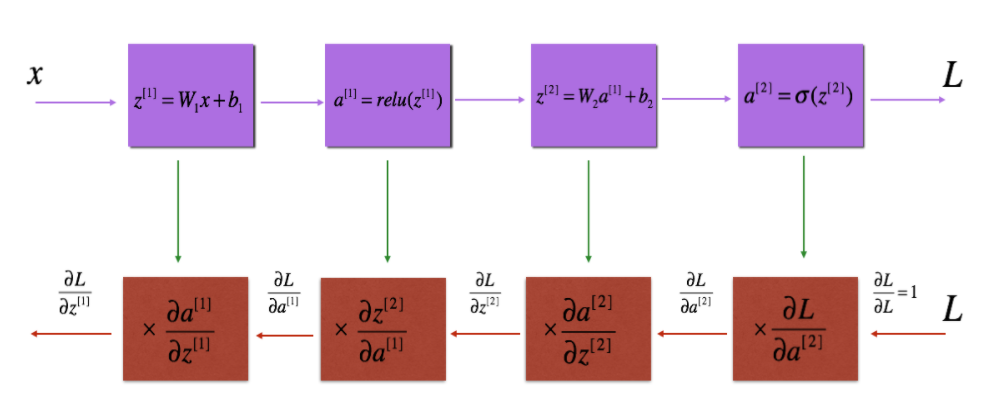
直接看一个最难的，结合上面的图与公式进行推导，

$$\frac{\partial J}{\partial w^{[1]}} = \frac{\partial J}{\partial a^{[2]}} \frac{\partial a^{[2]}}{\partial z^{[2]}} \frac{\partial z^{[2]}}{\partial a^{[1]}} \frac{\partial a^{[1]}}{\partial z^{[1]}} \frac{\partial z^{[1]}}{\partial w^{[1]}}$$

上面就是链式法则，显然要求$w^{[1]}$的偏导，首先要将前面的偏导数全部求出来， 一个一个的写出来。

首先对$a^{[2]}$进行求导，它是在上面的交叉熵函数里面，

$$\frac{\partial J}{\partial a^{[2]}} = \frac{1 - y}{1 - a^{[2]}} - \frac{y}{a^{[2]}}$$

再对$z^{[2]}$进行求导，它通过了一个sigmoid函数，

$$\frac{\partial a^{[2]}}{\partial z^{[2]}} = \frac{\partial}{\partial z^{[2]}}(\frac {1}{1+e^{-z^{[2]}}}) = a^{[2]}(1 - a^{[2]})$$

继续对$a^{[1]}$进行求导，它通过了一个线性运算，

$$\frac{\partial z^{[2]}}{\partial a^{[1]}} = \frac{\partial }{\partial a^{[1]}} (w^{[2]}a^{[1]} + b^{[2]}) = w^{[2]}$$

接着对$z^{[1]}$进行求导，这里通过了一个tanh运算，

$$\frac{\partial a^{[1]}}{\partial z^{[1]}} = \frac{\partial}{\partial z^{[1]}} (\frac{e^{z^{[1]}} - e^{-z^{[1]}}}{e^{z^{[1]}} + e^{-z^{[1]}}}) = 1 - (a^{[1]})^2$$

最后对$w^{[1]}$进行求导，这也是同样的一个线性运算，

$$\frac{\partial z^{[1]}}{\partial w^{[1]}} = \frac{\partial}{\partial w^{[1]}}(w^{[1]}x + b^{[1]}) = x$$

对于偏执$b^{[1]}, b^{[2]}$，它们的导数同理，可以写为，

$$\frac{\partial J}{\partial b^{[2]}} = \frac{\partial J}{\partial a^{[2]}} \frac{\partial a^{[2]}}{\partial z^{[2]}} \frac{\partial z^{[2]}}{\partial b^{[2]}}$$ $$\frac{\partial J}{\partial b^{[1]}} = \frac{\partial J}{\partial a^{[2]}} \frac{\partial a^{[2]}}{\partial z^{[2]}} \frac{\partial z^{[2]}}{\partial a^{[1]}} \frac{\partial a^{[1]}}{\partial z^{[1]}} \frac{\partial z^{[1]}}{\partial b^{[1]}}$$

其中，

$$\frac{\partial z^{[2]}}{\partial b^{[2]}} = 1$$ $$\frac{\partial z^{[1]}}{\partial b^{[1]}} = 1$$

---

综合上面的所有式子，可以将各个参数的导数写为，

$$\frac{\partial J}{\partial a^{[2]}} = \frac{1 - y}{1 - a^{[2]}} + \frac{y}{a^{[2]}}$$ $$\frac{\partial J}{\partial z^{[2]}} = \frac{\partial J}{\partial a^{[2]}} \frac{\partial a^{[2]}}{\partial z^{[2]}} = \frac{\partial J}{\partial a^{[2]}} a^{[2]}(1 - a^{[2]}) = a^{[2]} - y$$ $$\frac{\partial J}{\partial w^{[2]}} = \frac{\partial J}{\partial z^{[2]}} \frac{\partial z^{[2]}}{\partial w^{[2]}} = \frac{\partial J}{\partial z^{[2]}} a^{[1]} = (a^{[2]} - y)a^{[1]}$$ $$\frac{\partial J}{\partial b^{[2]}} = \frac{\partial J}{\partial z^{[2]}} \frac{\partial z^{[2]}}{\partial b^{[2]}} = \frac{\partial J}{\partial z^{[2]}} = a^{[2]} - y$$ $$\frac{\partial J}{\partial a^{[1]}} = \frac{\partial J}{\partial z^{[2]}} \frac{\partial z^{[2]}}{\partial a^{[1]}} = \frac{\partial J}{\partial z^{[2]}} w^{[2]} = (a^{[2]} - y)w^{[2]}$$ $$\frac{\partial J}{\partial z^{[1]}} = \frac{\partial J}{\partial a^{[1]}} \frac{\partial a^{[1]}}{\partial z^{[1]}} = \frac{\partial J}{\partial a^{[1]}} (1 - (a^{[1]})^2)$$ $$\frac{\partial J}{\partial w^{[1]}} = \frac{\partial J}{\partial z^{[1]}} \frac{\partial z^{[1]}}{\partial w^{[1]}} = \frac{\partial J}{\partial z^{[1]}} x$$ $$\frac{\partial J}{\partial b^{[1]}} = \frac{\partial J}{\partial z^{[1]}} \frac{\partial z^{[1]}}{\partial b^{[1]}} = \frac{\partial J}{\partial z^{[1]}}$$

---

所以在计算正向传播时，需要将中间计算得到的各个$a^{[i]}$的值保存下来， 因为在反向传播时，会用到它们。

在反向传播的计算中，一层一层从后向前计算梯度， 就可以利用链式法则计算出各个参数的梯度了。

参数更新：

这里先不引入高级的参数更新方式，就正常的更新，

$$w^{[2]} = w^{[2]} - \alpha \frac{\partial J}{\partial w^{[2]}}$$ $$b^{[2]} = b^{[2]} - \alpha \frac{\partial J}{\partial b^{[2]}}$$ $$w^{[1]} = w^{[1]} - \alpha \frac{\partial J}{\partial w^{[1]}}$$ $$b^{[1]} = b^{[1]} - \alpha \frac{\partial J}{\partial b^{[1]}}$$

---

更多层的神经网络

简单的理解，深度神经网络就是层数比较多的神经网络， 所以基本的操作可以说和上面的两层神经网络是一样的，

下面按照编程题过一遍整个流程，首先是网络结构图，

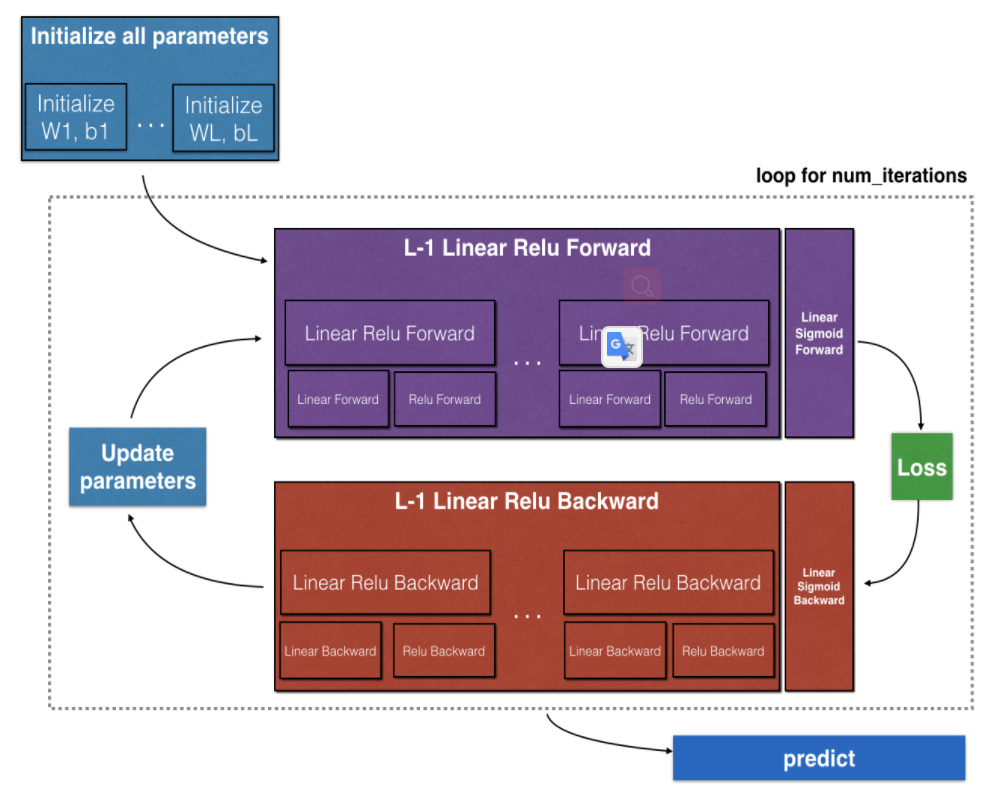
图中就是一个深度神经网络的结构，它中间神经元的激活函数是ReLU， 最后一层是由sigmoid神经元组成，这一般适用于进行多分类。

由图中，可以看出整个神经网络的一个训练步骤：

1. 初始化各层的权值$W$和$b$。
2. 输入样本，进行前向传播，先进过一系列的ReLU激活函数， 最后再通过一个sigmoid，得到最后得输出。
3. 对于得到的输出，计算它与样本的标签值的交叉熵，得到当前的损失。
4. 将损失反向传播。
5. 更新各个参数，继续从第2步开始。

注意在前向传播的过程中，要存下每一层的输出，因为在反向传播时需要用到它们。

各层参数的维度：

明白各层参数的维度，对于理解神经网络的代码很重要，这里写出它们的矩阵维度。

首先，假设一个输入样本是一个12288长度的行向量，它是由一幅64*64*3的图片展开而成的， 同时假设输入共有209个样本。

同时需要假设如下的一些东西：

• 网络一共有$L$层。
• 样本数$m = 209$。
• 样本维度$n = 12288$。
• 第$i$层的神经元数量有$n^{[i]}$个。
• 最后一层就是输出层，按上面的定义，它神经元的个数就是$n^{[L]}$个。

从输入开始，假设每个样本是一个列向量，那么输入就是一行输入样本，

$$X = \begin{bmatrix} x^{[1]} & x^{[2]} & ... & x^{[m-1]} & x^{[m]} \end{bmatrix}$$

其中$x^{[i]}$就是一个样本，它是一个列向量，

$$x^{[i]} = \begin{bmatrix} x_1^{[i]} \\ x_2^{[i]} \\ ... \\ x_{n-1}^{[i]} \\ x_n^{[i]} \end{bmatrix}$$

所以输入$X$的维度是，$X \in R^{n \times m}$。

为了方便线性运算，也就是之间$WX + b$来计算，这里把每个神经元定义为一个行向量， 并且它的长度等于它上一层的神经元数。

$$W^{[i](j)} = \begin{bmatrix} w_{1}^{[i](j)} & w_{2}^{[i](j)} & ... & w_{n^{[i-1]}-1}^{[i](j)} & w_{n^{[i-1]}}^{[i](j)} \end{bmatrix}$$

其中$W^{[i](j)}$就表示第$i$层的第$j$个神经元。那么对于$W^{[i]}$，它就等于，

$$W^{[i]} = \begin{bmatrix} W_1^{[i]} \\ W_2^{[i]} \\ ... \\ W_{n^{[i]}-1}^{[i]} \\ W_{n^{[i]}}^{[i]} \end{bmatrix}$$

所以第$i$层的神经元的权值矩阵$W^{[i]}$的维度为，$W^{[i]} \in R^{n^{[i]} \times n^{[i-1]}}$，另外，

$$z^{[i]} = W^{[i]}a^{[i-1]} + b \in R^{n^{[i]} \times m}$$ $$a^{[i]} = g(z^{[i]}) \in R^{n^{[i]} \times m}$$

---

将它们的维度总结如下，当然它们所对应的导数和它们的维度一致，

$$X \in R^{n \times m}$$ $$z^{[i]} \in R^{n^{[i]} \times m}$$ $$a^{[i]} \in R^{n^{[i]} \times m}$$ $$W^{[i]} \in R^{n^{[i]} \times n^{[i-1]}}$$ $$b^{[i]} \in R^{n^{[i]} \times 1}$$

---

前向传播：

只需要注意保存中间变量。

反向传播：

结合对两层神经网络的描述，其实反向传播的计算也很简单， 就从后向前计算导数就好了。

Hyperparameter：

超参数，就是一些需要在训练前就确定好的参数，并且可以认为一旦训练开始， 就不能再改变它们的值了，在神经网络中，超参数控制着$W$和$b$的最终取值， 可以认为它们决定了网络的最终性能。

例如下面的一些参数，

• 学习速率$\alpha$。
• 迭代次数$t$。
• 网络层数$L$。
• 某一层的神经元数$n^{[1]},n^{[2]},…$
• 激活函数的选择。

对于这样一些的参数的选择，通常情况都得按着经验来，现在的很多研究也都是围绕着如何调参来展开的。

一般情况只能一个一个的去试，看哪一组参数最合适，所以这是一个很耗时间的过程。

---

总结

第一个专项的课程，主要还是在于引入深度神经网络，讲了最为重要的前向传播和反向传播， 理解好前向与反向传播，对于神经网络的学习至关重要。